A Tangent is Perpendicular to a Radius and Diameter

A line tangent to a circle with center O at point P is perpendicular to the radius from O to P.

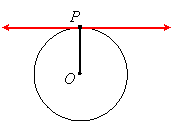If this were not true then we could draw a segment from O perpendicular to the line at some point Q:

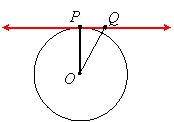Then triangle OQP would be a right triangle with Q as the right angle and therefore OP as the hypotenuse.  This would imply that OP is longer than OQ.  But that can't be since Q is outside the circle and therefore OQ is longer than the radius.

Since a diameter contains a radius, a line tangent to a circle is also perpendicular to the diameter that meets the point of tangency:

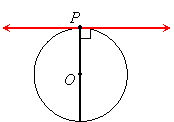 Example 1:  Determine whether line AB is tangent to circle O:

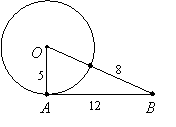Solution:  If it is tangent, then triangle OAB would be a right triangle.  Since the radius of the circle is 5 units, the hypotenuse would be OB = 5 + 8 = 13.  We check using the Pythagorean Theorem:  5² + 12² = 169 = 13².  Since a² + b² = c², it is a right triangle, so line AB is tangent to circle O.

toc | return to top | next page