Surface Area of a Sphere

From the formula for the volume of a sphere, it is easy to derive a formula for the surface area.  Imagine the sphere as a hollow rubber ball, like a tennis ball.  Here it is with a chunk removed:

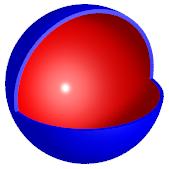
If the rubber is t units thick, then the volume of rubber is equal to the difference of the volumes of a sphere of radius r and a sphere of radius r – t:

We need to simplify this by expanding (r – t)³:

(r – t)³ = (r – t) (r – t) (r – t) = (r² – 2rt + t²)(r – t)

= r³ – 3r²t + 3rt² – t³

So

Now if the thickness of the rubber is t, then its volume is t times its area, so the area of the rubber must be:

If t is very small, then the last two terms are close to 0, and we are left with the surface area of the sphere:

toc | return to top | previous page | Home Page