Dimensions of a Slice

If the disc is t units thick, then its volume depends on its height, x, above the center of the sphere.  Since the disc is a cylinder, its volume is the area of its circular base times its thickness:

Now this volume is the difference of the volumes of two other discs of thickness t, and those discs can come from a cylinder of radius r and height 2r, and a double cone whose bases are also of radius r and whose total height is 2r:

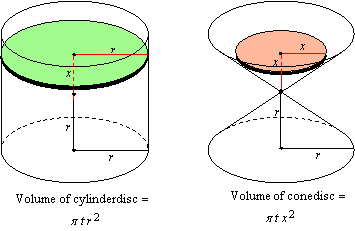
That is, the volume of the sphere disc at height x above the center is equal to the difference of the volumes of a cylinder disc and a cone disc at height x above the center.  Therefore, the volume of all the discs in the sphere is the difference of the volumes of all the discs in the cylinder and double cone:

toc | return to top | previous page | next page