Volume and Surface Area of a Sphere

Cavalieri's Principle

If two objects can be made from thousands of flat pieces of paper such that each piece of one of the objects has the same area as a corresponding piece of the other object, then the two objects must have the same volume. This is an intuitive way to think of Cavalieri's principle, and it is fundamental to understanding the formula for the volume of a sphere. What we do is compare slices of a sphere with slices of a hollowed-out cylinder. A circular slice from a sphere can have the same area as a ring that is a slice from a cylinder that has been hollowed out by two cones:

More precisely, Cavalieri's Principle says two three-dimensional solids have the same volume if they share the same cross-sectional areas at equal heights.

Slicing a Sphere 

Suppose we have a sphere of radius r:

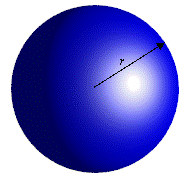
If we slice it with many horizontal planes, we can think of it as being composed of a large number of discs:

Consider one of these discs at a height x units above the center of the sphere:

Dimensions of a Slice

If the disc is t units thick, then its volume depends on its height, x, above the center of the sphere.  Since the disc is a cylinder, its volume is the area of its circular base times its thickness:

Now this volume is the difference of the volumes of two other discs of thickness t, and those discs can come from a cylinder of radius r and height 2r, and a double cone whose bases are also of radius r and whose total height is 2r:

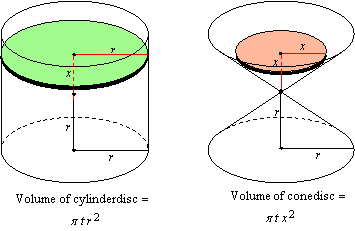
That is, the volume of the sphere disc at height x above the center is equal to the difference of the volumes of a cylinder disc and a cone disc at height x above the center.  Therefore, the volume of all the discs in the sphere is the difference of the volumes of all the discs in the cylinder and double cone:

The Volume of the Sphere

We already know how to find the volume of a cylinder and cone, so from these we can find the volume of a sphere.

Volume of cylinder of height 2r and radius r:  V_cylinder =  πr^{2 .} 2r = 2π r³

Volume of (single) cone of height r and radius r:  V_cone = 1/3 πr^{2 .} r = 1/3 πr³

Volume of cylinder hollowed out by a double cone:

V_{hollowcylinder} = 2π r³ – 2 ^. 1/3 πr³ = 6/3 πr³ – 2/3 2π r³ = 4/3π r³

The volume of the sphere is the same as the volume of the hollowed out cylinder:

Surface Area of a Sphere

From the formula for the volume of a sphere, it is easy to derive a formula for the surface area.  Image the sphere as a hollow rubber ball, like a tennis ball.  Here it is with a chunk removed:

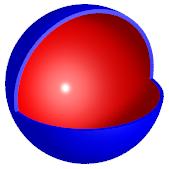
If the rubber is t units thick, then the volume of rubber is equal to the difference of the volumes of a sphere of radius r and a sphere of radius r – t:

We need to simplify this by expanding (r – t)³:

(r – t)³ = (r – t) (r – t) (r – t) = (r² – 2rt + t²)(r – t)

= r³ – 3r²t + 3rt² – t³

So

Now if the thickness of the rubber is t, then its volume is t times its area, so the area of the rubber must be:

If t is very small, then the last two terms are close to 0, and we are left with the surface area of the sphere:

Return to Lesson 12