Regular Polygons

For a regular polygon, the center of the inscribed circle is the intersection of the angle bisectors, and a radius can be found by constructing a perpendicular from the center to a side.  If the polygon has an even number of sides, the center is also the common intersection of the diagonals.  The radius of the incircle is called the apothem.  

The formula for the area of a regular polygon is often given as

where p is the perimeter and a is the apothem.  This follows from the fact that the area of a triangle is half its base times its height, and the height is the apothem:

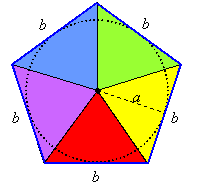
The area of each triangle is ½ ba, where a is the apothem.  Multiplying by the number of triangles transforms this formula to ½ pa, where p = nb and n is the number of sides of the regular polygon (in the above picture, n = 5).

 

toc | return to top | previous page