Inscribed Circles

The Incircle of a Triangle

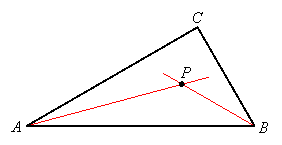
A circle is inscribed in a triangle when it is tangent to the three sides of the triangle.  Such a circle is called the triangle's "incircle."  Its center is equidistant from the sides of the triangle and is the common intersection of the bisectors of the angles of the triangle:

Proof:  Let ABC be a triangle and let AP and BP be the bisectors of angles A and B:

Let D be the point on side AB where a perpendicular from P intersects that side, let E be the point on side AC where a perpendicular from P intersects that side, and let F be the point on side BC where a perpendicular from P intersects that side:

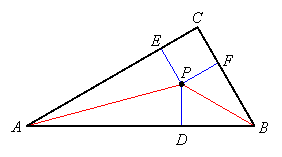
Then DP = EP since AP bisects angle A and DP = FP since BP bisects angle B.  Therefore EP = FP, and so P is equidistant from sides AC and BC.  Thus P is on the bisector of angle C, so the three angle bisectors are concurrent at point P, and this is the center of the incircle:

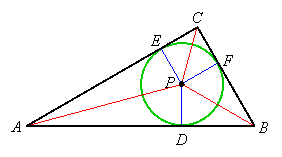
Incircles of Polygons

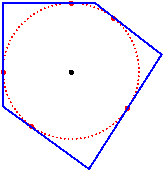
A circle is inscribed in a polygon if it is tangent to each of the sides of the polygon.  Such a circle is called an "incircle."  Most polygons do not have incircles, but regular polygons do.  We can construct a nonregular polygon that has an incircle by choosing points of tangency on the circle and then constructing the tangent lines whose intersections are the vertices of the polygon.  For example, we could construct a nonregular pentagon with an incircle by randomly choosing 5 points on the circumference of the circle, not all on the same semicircle, and constructing tangents at these points:

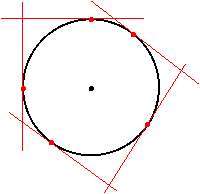
The resulting pentagon has the given circle as its incircle:

Regular Polygons

For a regular polygon, the center of the inscribed circle is the intersection of the angle bisectors, and a radius can be found by constructing a perpendicular from the center to a side.  If the polygon has an even number of sides, the center is also the common intersection of the diagonals.  The radius of the incircle is called the apothem.  

The formula for the area of a regular polygon is often given as

where p is the perimeter and a is the apothem.  This follows from the fact that the area of a triangle is half its base times its height, and the height is the apothem:

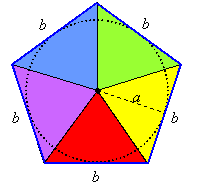
The area of each triangle is ½ ba, where a is the apothem.  Multiplying by the number of triangles transforms this formula to ½ bp, where p = nb and n is the number of sides of the regular polygon (in the above picture, n = 5).

Return to Lesson 8