- Next
- Page 1 of 3
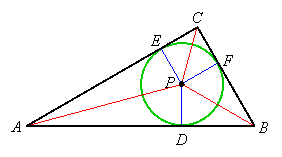
The Incircle of a Triangle
A circle is inscribed in a triangle when it is tangent to the three sides of the triangle. Such a circle is called the triangle's "incircle." Its center is equidistant from the sides of the triangle and is the common intersection of the bisectors of the angles of the triangle:
Proof: Let ABC be a triangle and let AP and BP be the bisectors of angles A and B:
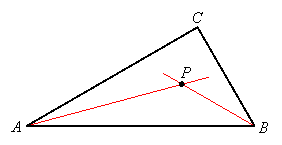
Let D be the point on side AB where a perpendicular from P intersects that side, let E be the point on side AC where a perpendicular from P intersects that side, and let F be the point on side BC where a perpendicular from P intersects that side:
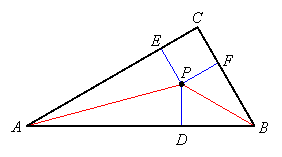
Then DP = EP since AP bisects angle A and DP = FP since BP bisects angle B. Therefore EP = FP, and so P is equidistant from sides AC and BC. Thus P is on the bisector of angle C, so the three angle bisectors are concurrent at point P, and this is the center of the incircle: