Copy an Angle

If you given an angle and ray that is supposed to be one side of another angle that is congruent to the given angle, you can use SSS congruence of triangles to make a copy.  What you do is make the given angle into a triangle by marking off two points on its sides (you don't actually have to draw the third side, though), and then copy one of those "sides" to the given ray and determine the vertex of the other "side."

The easiest way is to make both "sides" the same length, like this:

Given:  Angle A and ray with vertex P:

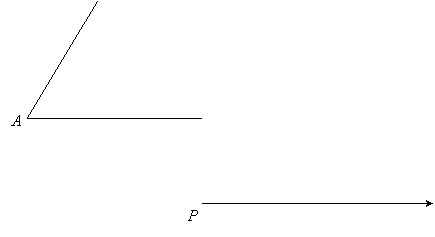Construct angle QPR congruent to angle A.

Solution:

First set the compass at any convenient length, mark off points B and C on angle A, and make a similar arc of the circle with center P on the given ray. Let Q be the intersection of that arc with the ray:

Then set the compass to measure the distance from B to C (this distance is the length of the "third side" of triangle ABC), then place the point of the compass at Q and mark off that distance on the arc there to locate point R:

Finally, draw the ray from P to R.  Then angle QPR is congruent to angle BAC since triangles QPR and BAC are congruent by SSS.

Here is an animation of this construction.

toc | return to top | previous page | next page