Basic Constructions

Tools for Constructions

We have previously used rulers and protractors to measure segments and angles, and sometimes to draw geometric figures.  In these lessons you will learn how to draw accurate geometric figures using only a straight-edge and a compass.  A ruler is a straight-edge, but you will not need the units in most cases.

A straight-edge is used to construct a line (or a segment) that contains two given points.  That one and only one such line exists is one of the postulates of Euclidean geometry.

A compass is used to draw a circle when given two points, one being its center and the other being a point on its circumference.  By definition, a circle is the set of all points equidistant from the center.

You will need a compass and straight-edge for the homework with these lessons.  Any simple ruler will do as a straight-edge, and an inexpensive compass, such as that shown below, will work fine.

There is a website (the link is given at the bottom of each page containing a construction) that uses java programs to animate all of the constructions we will consider, so if you have trouble understanding any of them, please go to that link.

Further information on constructions can be found here.  

Copy a Segment

Our first construction is the easiest:

Given segment AB, construct another segment CD that is congruent to AB: 

The way to do it is to make a circle with radius AB and center C, choose any point on the circumference as point D, and then draw the segment CD. 

First set the compass:  place the point of the compass at point A and set it so the pencil is on point B.  This way you measure the correct radius.  Then use the straight-edge to draw a line (rather, a segment) that is clearly longer than AB.  Label point C on the left of the line and place the point of the compass there.  Finally, sweep out an arc that intersects the line.  The point of intersection is point D:

Use the compass to "measure" AB:

Place the point at C and sweep out an arc of a circle of radius AB:

Here is an animation of this process.

Find the Midpoint of a Segment

This is also called "bisecting a segment," and this construction actually produces the perpendicular bisector of a segment.  It makes use of the theorem which states that the perpendicular bisector of a segment consists of points that are equidistant from the endpoints of the segment.

Given segment AB, construct the perpendicular bisector of that segment.

Solution:  Place the point of the compass at A and open it to any convenient length more than half of the segment (but not as long as the segment), and sweep out an arc:

Then place the point of the compass at B, keeping the same radius, and sweep out another arc:

Finally use the straight-edge to draw a line through the two points where the arcs cross:

That line is the perpendicular bisector of segment AB, crossing it at its midpoint, M.

Here is an animation of this process.

Copy an Angle

If you given an angle and ray that is supposed to be one side of another angle that is congruent to the given angle, you can use SSS congruence of triangles to make a copy.  What you do is make the given angle into a triangle by marking off two points on its sides (you don't actually have to draw the third side, though), and then copy one of those "sides" to the given ray and determine the vertex of the other "side."

The easiest way is to make both "sides" the same length, like this:

Given:  Angle A and ray with vertex P:

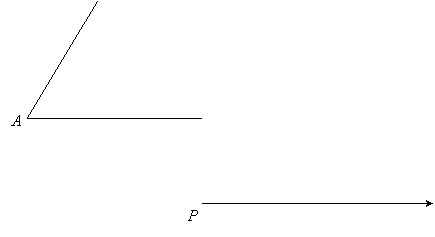Construct angle QPR congruent to angle A.

Solution:

First set the compass at any convenient length, mark off points B and C on angle A, and make a similar arc of the circle with center P on the given ray. Let Q be the intersection of that arc with the ray:

Then set the compass to measure the distance from B to C (this distance is the length of the "third side" of triangle ABC), then place the point of the compass at Q and mark off that distance on the arc there to locate point R:

Finally, draw the ray from P to R.  Then angle QPR is congruent to angle BAC since triangles QPR and BAC are congruent by SSS.

Here is an animation of this construction.

Bisect an Angle

The easiest way to bisect an angle is to make a kite.  A kite in geometry is a quadrilateral with two pairs of adjacent congruent sides.  The diagonal joining the vertices where the congruent sides meet each other bisects both angles formed by those sides:

In this kite, AB = AD and BC = DC.  Diagonal AD bisects angle BAD and BCD.

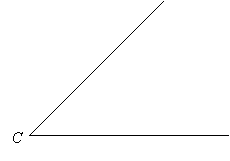
Suppose C is a given angle you want to bisect. 

First you mark off segments CB and CD with the compass set to any convenient length:

Then you locate point A so it is equidistant from B and D:

Finally draw the bisector, CA:

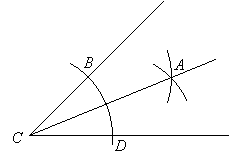
Here is an animation of this construction.

Return to Lesson 10