A county plans to build a new water plant on the shore of a long lake.  Water will be piped to two different water towers located according to the following map:

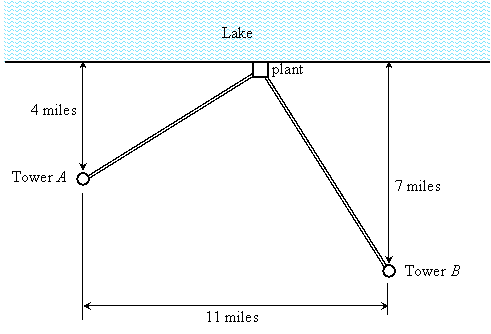
Where should the plant be located so the sum of the distances from the two water towers is as small as possible?

Solution:

Extend the vertical line from Tower A into the lake an equal distance beyond the shore-line to point Q, then draw a segment from Q to Tower B, and let P be the point where this segment crosses the shore-line.  Then draw a segment from P to A:

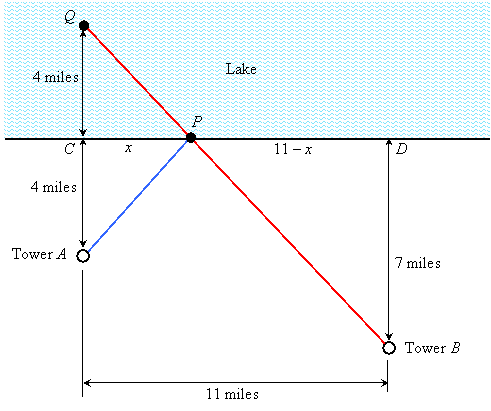
Notice that segments QP and AP have the same length.  In addition, QB is the shortest distance from Q to B.  But QB = QP + PB = AP + PB.  So the water plant should be located at point P.

To find distances, notice that the right triangles QCP and BDP are similar (because the vertical angles at P are congruent), so we can solve the following ratio to find x:

Cross-multiply:  , so , and x = 4.  So the water plant should be located 4 miles right of where the perpendicular from Tower A meets the shore-line.