Triangle Inequalities

The Exterior Angle Theorem

In Euclidean geometry, the sum of the angles of any triangle is 180o.  If you extend one side of a triangle, you get an exterior angle that is supplementary to its adjacent, interior angle:

The other two interior angles are called remote interior angles since they are "remote" from the exterior angle, and since all three angles of the triangle add to 180o, these remote interior angles add to the exterior angle.  In other words, we have:

The Exterior Angle Theorem

The measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles. 

Proof:

Let the triangle be  and the exterior angle be :

Then we need to prove that .  Since the exterior angle,  is supplementary to its adjacent interior angle, , we know , so .  But we also know the angles in the triangle add to 180o:  , so .  Since  and  are both equal to , they are equal to each other by the transitive property:  .

Here is an obvious result that follows immediately:

Corollary to the Exterior Angle Theorem

The measure of an exterior angle is always greater than the measure of either remote interior angle.

Proof:

In the above setup, .  If we drop one of the measures on the right, we have  or  since angles always have positive measure.

Relation between Angles and Sides of a Triangle

An important consequence of the corollary to the exterior angle theorem is this:

Theorem 1:

If one side of a triangle is longer than a second side, then the angle opposite the first side is greater than the angle opposite the second side.

Proof:

Label the triangle as with , place point  on side  so , and draw segment :

Because , .  But  is isosceles, so , so  (by substitution).  Because  is an exterior angle of , it is greater than the remote interior angle A:  .  So we have:

  and 

And by the transitive property for inequalities, it follows that .  But  is the angle opposite the longer side, , and  is the angle opposite the shorter side, .  Thus the angle opposite the longer side is greater than the angle opposite the shorter side.

The converse of this theorem is also true:

Theorem 2:

If one angle of a triangle is larger than a second angle, then the side opposite the first angle is longer than the side opposite the second angle.

Proof:

It is easier to prove the contrapositive of this statement:

If one side of a triangle, , is not longer than a second side, ,  then the angle opposite the first side,  is not larger than the angle opposite the second side, .

So we assume in  that side  is not longer than side .  Then either it is the same length, or it is shorter.  If it is the same length, then we have an isosceles triangle, so .  Therefore  is not larger than .

 

If  is shorter than side , then by Theorem 1, :

Is it obvious which side of a triangle is longest?

It might seem silly to have to prove these results.  If you look at the pictures, they seem rather obvious.  However, if the triangle is "almost equilateral," then it is not so obvious:

Example:

Which side is the longest side in this triangle?

Solution:

We first find the measure of angle Q:

,  so

So  is the largest angle, and therefore  is the longest side.

Shortest Distance

Two results follow from Theorems 1 and 2:

Corollary 1:

The shortest distance from a point to a line is the length of the perpendicular segment from that point to that line.

Proof:

Let  be a point not on the line, let  be the perpendicular segment from  to the line, and suppose point  is some other point on the line.  Draw segment .  Then  is a right triangle with .  Since the angles of a triangle add to 180o, the other two angles in this triangle must be less than 90o.  Therefore, , so the opposite sides have the same inequality:  .  That is, any other segment from  to the line is longer than .

Corollary 2:

The perpendicular segment from a point to a plane is the shortest distance from that point to the plane.

Proof:

Let  be a point not in the plane, let  be the perpendicular segment from  to the plane, and suppose point  is some other point in the plane.  Then  is shorter than  because it is the shortest segment to line , by Corollary 1.

 

The Triangle Inequality

It is well-known that the shortest distance between two points is along a straight line.  This is actually a statement about side-lengths of triangles, and is not a postulate in Euclidean geometry since it follows from other postulates:

Theorem: 

The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Proof:

In any triangle either all sides are the same length, or one side is longer than at least one other side.  Call the "longest side"  and let  be the third vertex.  Then we already know that  and .  Therefore (if we add another length to ) we know that  and .  So all we have to prove is that .

Draw the perpendicular segment  to side .  Then by Corollary 1,  is the shortest distance from point  to  and  is the shortest distance from point  to , so and and therefore .  But since  is between  and , .  Therefore,  by substitution.

 

Example:

The lengths of two sides of a triangle are 5 and 8.  Between which two numbers must the length of the third side be?

Solution:

If the length of the third side is x, then each of the following inequalities must be true:

x + 5 > 8,  x + 8 > 5, and 5 + 8  > x.  These simplify to:

x > 3,  x > –3, and 13 > x.  The middle inequality tells us nothing, but the other two tell us x is between 3 and 13.  That is, the length of the third side must be between the sum and difference of the lengths of the other two.

 

Application

A county plans to build a new water plant on the shore of a long lake.  Water will be piped to two different water towers located according to the following map:

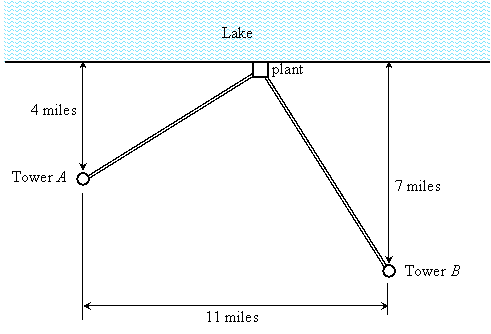
Where should the plant be located so the sum of the distances from the two water towers is as small as possible?

Solution:

Extend the vertical line from Tower A into the lake an equal distance beyond the shore-line to point Q, then draw a segment from Q to Tower B, and let P be the point where this segment crosses the shore-line.  Then draw a segment from P to A:

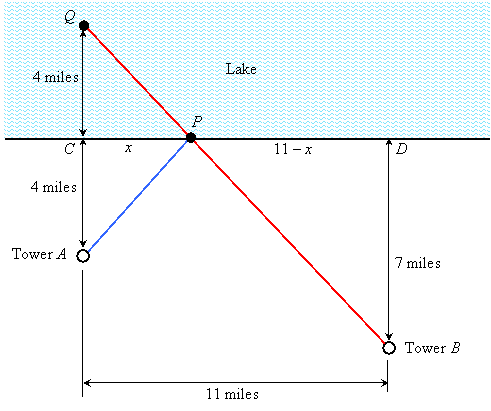
Notice that segments QP and AP have the same length.  In addition, QB is the shortest distance from Q to B.  But QB = QP + PB = AP + PB.  So the water plant should be located at point P.

To find distances, notice that the right triangles QCP and BDP are similar (because the vertical angles at P are congruent), so we can solve the following ratio to find x:

Cross-multiply:  , so , and x = 4.  So the water plant should be located 4 miles right of where the perpendicular from Tower A meets the shore-line.