Exact Answers

 As you learned in Lesson 2, it is sometimes desirable to give "exact answers" for the sides of triangles.  This means the lengths are given as whole numbers, fractions, or simplified square roots.  Since the square root of a product is the product of the square roots, a square root of a whole number can sometimes be "simplified" by breaking the number inside into the product of a perfect square and another whole number.  The following example shows how to simplify a square root:

EXAMPLE 5:       Simplify

SOLUTION:        We wish to factor 567 into the product of the largest perfect square we can find and another whole number.  First we list perfect squares no larger than half of 567:

                     Number             Perfect Square

                           1                            1

                           2                            4

                           3                            9

                           4                           16

                           5                           25

                           6                           36

                           7                           49

                           8                           64

                           9                           81

                         10                         100

                         11                         121

                         12                         144

                         13                         169

                         14                         196

                         15                         225

                         16                         256

Then we start at the bottom of the Perfect Square list and work our way upward to find the largest perfect square that divides 567 evenly.  We eliminate 256, 225, 196, 169, 144, 121, and 100 before we discover that 81 works:  .  Thus, , so .

EXAMPLE 6:

Find the simplified exact length of side  in the triangle on the right.

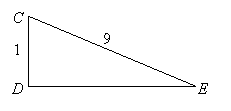SOLUTION:   Let DE = x.  By the Pythagorean Theorem, .  So , .  Now we need to simplify :  We start by listing the perfect squares less than 40.  They are 1, 4, 9, 16, 25, 36.  36 and 25 do not go into 80, but 16 does:  , so  and  = .  That is, .

toc | return to top | previous page