Examples of 30-60-90 Triangles 

EXAMPLE 1:

Find the exact length of the side marked x in the triangle on the right: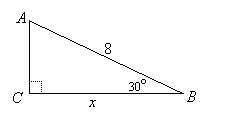

SOLUTION:        "Exact" means we must give a simplified answer involving square roots.  In this triangle, side  is the hypotenuse, so we set its length to 2a:  8 = 2a.  Thus, a = 4, and since side  is adjacent the 30^o angle, its length is , so in this case .

EXAMPLE 2:

Find the exact length of the hypotenuse in this right triangle: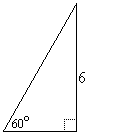

SOLUTION:

Comparing with a standard 30-60-90 triangle, the given side is , so , and .  We need to simplify this by rationalizing the denominator.  We do that by multiplying top and bottom by :  .  The hypotenuse is .

toc | return to top | previous page | next page