Special Right Triangles

30-60-90 Triangles

An equilateral triangle is a triangle with all sides congruent.  From the Isosceles Triangle Theorem if follows that the angles of an equilateral triangle are all the same.  Since the angles of any triangle add to 180^o, each angle of an equilateral triangle must be 60^o.  When an equilateral triangle is cut in half, you get two right triangles.  The acute angles of these triangles are 30^o and 60^o, so we call them "30-60-90 triangles": 

If a side of the equilateral triangle is 2 units in length, then the side opposite the 30^o angle in one of the 30-60-90 triangles is half that, or 1 unit, and the third side (the side opposite the 60^o angle) can be found by the Pythagorean Theorem:

In general, in a 30-60-90 triangle, the side opposite the 30^o angle is half the hypotenuse.  The other side can then be found by the Pythagorean Theorem, and will always be a multiple of the square root of 3.  More specifically, let the length of the hypotenuse be 2a.  Then the side opposite the 30^o angle will be of length a, and we can find the third side as follows:

Notice that we can simplify  by separating into the product of two square roots:

.

Examples of 30-60-90 Triangles 

EXAMPLE 1:

Find the exact length of the side marked x in the triangle on the right: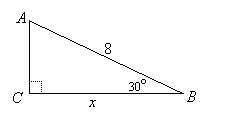

SOLUTION:        "Exact" means we must give a simplified answer involving square roots.  In this triangle, side  is the hypotenuse, so we set its length to 2a:  8 = 2a.  Thus, a = 4, and since side  is adjacent the 30^o angle, its length is , so in this case .

EXAMPLE 2:

Find the exact length of the hypotenuse in this right triangle: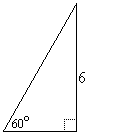

SOLUTION:

Comparing with a standard 30-60-90 triangle, the given side is , so , and .  We need to simplify this by rationalizing the denominator.  We do that by multiplying top and bottom by :  .  The hypotenuse is .

45-45-90 Triangles

Another special right triangle results when you cut a square in half using one of its diagonals.  Such a triangle is called a 45-45-90 triangle, because half each of 90^o angle is a 45^o angle:

Since the sides of a square are equal, we can label each leg of a 45-45-90 triangle as a.  Then the hypotenuse can be found by the Pythagorean Theorem:  ,  , .

Example of a 45-45-90 Triangle

EXAMPLE 3:

Find the length of the hypotenuse of a 45-45-90 triangle whose legs are each  in length.

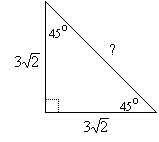SOLUTION:          In this case , so the hypotenuse

                              is .

Integer Right Triangles

 Another kind of special right triangle is an "integer right triangle."  That is a right triangle whose side-lengths are whole numbers.  The converse of the Pythagorean Theorem happens to be true (and can easily be proved from SSS).  That is, if the sides of a triangle are a, b and c, and  then the triangle is a right triangle.  When a, b and c are whole numbers then the triangle is an integer right triangle and the triple (a, b, c) is called a "Pythagorean Triple," as you learned in Lesson 2.

 The most "primitive" Pythagorean triple is (3, 4, 5).  Any common multiple of these numbers is also a Pythagorean triple.  That is, if k is any whole number, then (3k, 4k, 5k) is a Pythagorean triple, because:      

For example, (6, 8, 10) and (9, 12, 15) are Pythagorean triples.

 Other Pythagorean triples are (5, 12, 13), (8, 15, 17) and (7, 24, 25).  In fact, if m and n are whole numbers and m > n, then  is a Pythagorean triple, as can be verified using algebra.

Examples of Integer Right Triangles

EXAMPLE 4:

What is the measure of angle Q in the triangle on the right?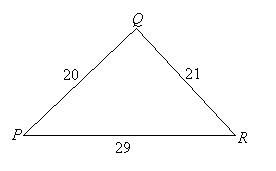

 SOLUTION:  This is not an isosceles or equilateral triangle, and we know only the side-lengths, so the answer is not obvious, but it might be a right triangle.  If we let c be the largest side-length and a and b the others, we check to see if :

?

 400 + 441 = 841

 841    =  841

It is a right triangle, and  is the hypotenuse.  Therefore angle Q is 90^o.

Exact Answers

 As you learned in Lesson 2, it is sometimes desirable to give "exact answers" for the sides of triangles.  This means the lengths are given as whole numbers, fractions, or simplified square roots.  Since the square root of a product is the product of the square roots, a square root of a whole number can sometimes be "simplified" by breaking the number inside into the product of a perfect square and another whole number.  The following example shows how to simplify a square root:

EXAMPLE 5:       Simplify

SOLUTION:        We wish to factor 567 into the product of the largest perfect square we can find and another whole number.  First we list perfect squares no larger than half of 567:

                     Number             Perfect Square

                           1                            1

                           2                            4

                           3                            9

                           4                           16

                           5                           25

                           6                           36

                           7                           49

                           8                           64

                           9                           81

                         10                         100

                         11                         121

                         12                         144

                         13                         169

                         14                         196

                         15                         225

                         16                         256

Then we start at the bottom of the Perfect Square list and work our way upward to find the largest perfect square that divides 567 evenly.  We eliminate 256, 225, 196, 169, 144, 121, and 100 before we discover that 81 works:  .  Thus, , so .

EXAMPLE 6:

Find the simplified exact length of side  in the triangle on the right.

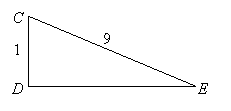SOLUTION:   Let DE = x.  By the Pythagorean Theorem, .  So , .  Now we need to simplify :  We start by listing the perfect squares less than 40.  They are 1, 4, 9, 16, 25, 36.  36 and 25 do not go into 80, but 16 does:  , so  and  = .  That is, .