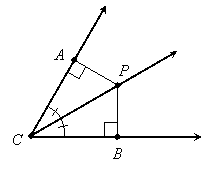
The Angle Bisector Theorem

If a point interior to an angle is equidistant from its sides, then that point is on the bisector of that angle, and conversely.

 Again we have a statement and its converse to prove:

 Statement:

If , , and  then  bisects .

 

Proof:

From the hypothesis,  and  are right triangles with congruent legs .  They also share a common hypotenuse:  .  Therefore  by HL.  Thus  since they are corresponding parts of the congruent triangles.  So  bisects  since this is the definition of "bisects."

Converse:

If  bisects , , and  then .

 

Proof:

Since  bisects ,  (by definition of "bisects").  In addition,  and  are right triangles with common side .  So  by AAS.  Therefore  since these are corresponding parts of the congruent triangles.

toc | return to top | previous page | next page