Right Triangles

HL

SSA or ASS is not a theorem in geometry because two triangles that are not congruent can satisfy this condition: 

 However, if the angle is a right angle, then the triangles are congruent.  This is a theorem, called HL for "hypotenuse-leg."

Theorem (HL): 

If two right triangles have congruent hypotenuse's and a pair of congruent legs, then the triangles are congruent.

We can prove this theorem by setting up two triangles that satisfy the HL hypothesis:

Given:   and  are right angles, , and

Prove: 

Proof:

Let  be a point on the ray opposite  so that , and draw  as in the picture on the right.  Because  is a right angle,  is also a right angle, and therefore congruent to .  So  by SAS.  

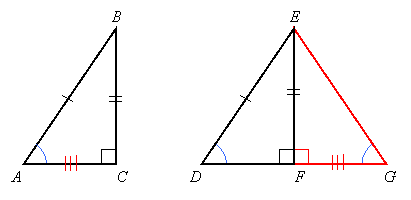
Therefore .  Since , the transitive property tells us that .  That shows  is isosceles, so .. Since , , and (using the transitive property again), .    Now we can conclude that  by SAA.

The Perpendicular Bisector Theorem

We have discussed this before, and now we will give a precise proof:

If a point is equidistant from the endpoints of a segment then it is on the perpendicular bisector of that segment, and conversely.

There are two things to prove here, a statement and its converse, so we will split the proof into two parts, using generic diagrams for each.

 Statement:

If  then  is on the perpendicular bisector of .

Proof:

Let  be the midpoint of  and draw :

Then  by SSS.  Therefore  since these are corresponding parts of the congruent triangles.  But these angles are a linear pair, so their measures add to 180^o.  Since they are congruent angles, each must measure half of 180^o, which is 90^o.  Therefore .  So  is on the perpendicular bisector of  (by definition of "perpendicular bisector").

Converse:

If  is the perpendicular bisector of  then .

Proof:

Because  is the perpendicular bisector of , , and  since both are right angles.   is a common side to  and , so these triangles are congruent by SAS.  Therefore  since they are corresponding parts of the congruent triangles.

The Angle Bisector Theorem

If a point interior to an angle is equidistant from its sides, then that point is on the bisector of that angle, and conversely.

 Again we have a statement and its converse to prove:

 Statement:

If , , and  then  bisects .

Proof:

From the hypothesis,  and  are right triangles with congruent legs .  They also share a common hypotenuse:  .  Therefore  by HL.  Thus  since they are corresponding parts of the congruent triangles.  So  bisects  since this is the definition of "bisects."

Converse:

If  bisects , , and  then .

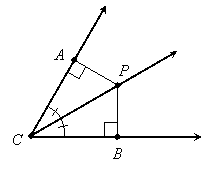
Proof:

Since  bisects ,  (by definition of "bisects").  In addition,  and  are right triangles with common side .  So  by AAS.  Therefore  since these are corresponding parts of the congruent triangles.

 The Angle Bisector Theorem for Isosceles Triangles

 In an isosceles triangle the bisector of the vertex angle cuts the opposite side in half.

 Note:  The vertex angle of an isosceles triangle is the angle which is opposite a side that might not be congruent to another side.

 To prove this, we rephrase it with a generic isosceles triangle:

If  and  bisects  then .

Proof:

Since  bisects , .   and  share a common side, , and it is given in the hypothesis that .  Therefore  by SAS.  As a consequence,  since these are corresponding sides of the congruent triangles.  So the lengths .  But  by the segment addition postulate, and therefore  (using substitution in algebra).

Something to Think About

If the triangle were not isosceles, then would an angle bisector cut the opposite side in half? For example, if  and  bisects  then is it still true that ?

The answer is no as you might notice from the diagram.  We will see in a later lesson after we discuss similar figures that  and  are proportional in the same way that the sides  and  are.