HL

SSA or ASS is not a theorem in geometry because two triangles that are not congruent can satisfy this condition: 

 

 However, if the angle is a right angle, then the triangles are congruent.  This is a theorem, called HL for "hypotenuse-leg."

Theorem (HL): 

If two right triangles have congruent hypotenuse's and a pair of congruent legs, then the triangles are congruent.

We can prove this theorem by setting up two triangles that satisfy the HL hypothesis:

Given:   and  are right angles, , and

Prove: 

Proof:

Let  be a point on the ray opposite  so that , and draw  as in the picture on the right.  Because  is a right angle,  is also a right angle, and therefore congruent to .  So  by SAS.  

 

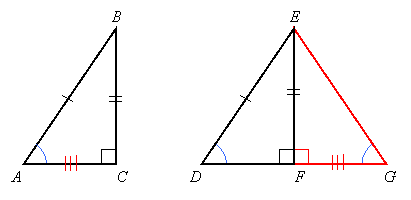
Therefore .  Since , the transitive property tells us that .  That shows  is isosceles, so .. Since , , and (using the transitive property again), .    Now we can conclude that  by SAA.

toc | return to top | next page