Results about quadrilaterals are usually proved by splitting the quadrilateral into triangles and using SSS, SAS or ASA to prove the triangles congruent.  For example, to prove that opposite sides of a parallelogram are congruent, we would draw a single diagonal and then prove the two resulting triangles are congruent by ASA, from which the result follows since the sides of the parallelogram are corresponding parts of the congruent triangles.

There is an important theorem about the midsegment of a trapezoid that should be discussed separately.  Recall the following result about a midsegment of a triangle:

A midsegment of a triangle is a segment joining the midpoints of two sides.  It is parallel to the third side and half its length:

From this theorem, we can derive a similar result for trapezoids.   The midsegment of a trapezoid is the segment joining the midpoints of its legs:

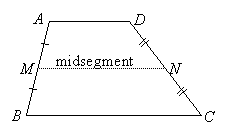
Since parallel lines cut transversals (which are the legs of the trapezoid) into proportional segments, it follows that the midsegment is parallel to the bases.  To see how the length of the midsegment is related to the lengths of the bases,  draw segment  parallel to leg , intersecting  at Q. 

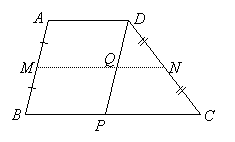
Then  is a midsegment of , so . But ADPB and ADQM are parallelograms, so MQ = AD and BP = AD, and since MN = MQ + QN and BC = BP + PC, we have:  MN = AD + QN, and BC = AD + 2QN.  That is, the lengths AD, MN and BC are in an arithmetic progression, which means they are equally spaced on the number line.  Another way to say this is:  MN is half-way between AD and BC.  We also call MN the average of AD and BC, and from algebra you recall that we can find an average of two numbers by adding them and dividing by 2.

EXAMPLE:

Find the length of the midsegment in the trapezoid on the right.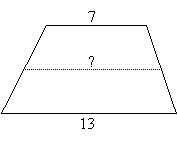

 SOLUTION:     One way to solve this is plot 7 and 13 on the number-line and find the number half-way between them:

The midsegment is 10 units long.

 Another way is to add 7 and 13, and divide by 2:  midsegment = .