Some of this can be broken down if we separate the result into two simpler results:

THEOREM 1:     If opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

THEOREM 2:     If the diagonals of a parallelogram are congruent, then that parallelogram is a rectangle.

Parallelograms and rectangles are special quadrilaterals, and their definitions are:

DEFINITION:      A parallelogram is a quadrilateral in which opposite sides are parallel.

DEFINITION:      A rectangle is a quadrilateral in which each interior angle is a right triangle.

Some additional theorems that can easily be proved about parallelograms and rectangles using congruent triangles that result when a diagonal is drawn are:

THEOREM 3:     If a pair opposite sides of a quadrilateral are congruent and parallel, then the quadrilateral is a parallelogram.

THEOREM 4:     A rectangle is a parallelogram.  (That is, the opposite sides of a rectangle are parallel.)

THEOREM 5:     If one angle of a parallelogram is a right angle, then the parallelogram is a rectangle.

THEOREM 6:     Opposite sides of a rectangle are congruent.

Now suppose a carpenter measures the left and right sides of a door frame and they are the same length, and he measures the diagonals and they too are the same length, but he fails to measure the top and bottom.  Is it possible that the door frame is not a true rectangle?  The following diagram shows that it might not be a rectangle:

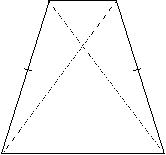
This figure is also a special quadrilateral.  It is called an isosceles trapezoid.