Quadrilaterals

The Rectangle

A quadrilateral is a 4-sided polygon.  Windows and doors are special quadrilaterals called rectangles.  Carpenters have a method of making sure the frames of windows and doors are indeed rectangles (have right angles).  If the sides are the same length and the top and bottom are the same, they measure the diagonals to see it they are also the same.  This method works very well, and is based on the following theorem:

THEOREM:     If opposite sides of a quadrilateral are congruent and the diagonals are congruent, then that quadrilateral is a rectangle.

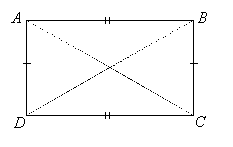
To prove it, suppose , , and diagonal  is congruent to diagonal  in quadrilateral ABCD.  Then by SSS, triangles ADC and CBA are congruent, so  and .  Since  and  are alternate interior angles for  and  with transversal , and  and  are alternate interior angles for  and  with transversal , it follows that the opposite sides of the quadrilateral are parallel (thus it is a parallelogram).  Also by SSS, , so .  But these are same-side interior angles for parallel lines  and , and therefore add to 180^o.  Since they are equal, each must be 90^o.  By the same reasoning, we conclude that the other two angles of the quadrilateral are right angles.

Parallelograms vs Rectangles

Some of this can be broken down if we separate the result into two simpler results:

THEOREM 1:     If opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

THEOREM 2:     If the diagonals of a parallelogram are congruent, then that parallelogram is a rectangle.

Parallelograms and rectangles are special quadrilaterals, and their definitions are:

DEFINITION:      A parallelogram is a quadrilateral in which opposite sides are parallel.

DEFINITION:      A rectangle is a quadrilateral in which each interior angle is a right triangle.

Some additional theorems that can easily be proved about parallelograms and rectangles using congruent triangles that result when a diagonal is drawn are:

THEOREM 3:     If a pair opposite sides of a quadrilateral are congruent and parallel, then the quadrilateral is a parallelogram.

THEOREM 4:     A rectangle is a parallelogram.  (That is, the opposite sides of a rectangle are parallel.)

THEOREM 5:     If one angle of a parallelogram is a right angle, then the parallelogram is a rectangle.

THEOREM 6:     Opposite sides of a rectangle are congruent.

Now suppose a carpenter measures the left and right sides of a door frame and they are the same length, and he measures the diagonals and they too are the same length, but he fails to measure the top and bottom.  Is it possible that the door frame is not a true rectangle?  The following diagram shows that it might not be a rectangle:

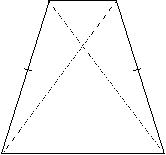
This figure is also a special quadrilateral.  It is called an isosceles trapezoid.

Trapezoids

DEFINITION:    A trapezoid is a quadrilateral in which a pair of opposite sides are parallel.  The parallel sides are called the bases of the trapezoid, and the other two sides are called its legs.

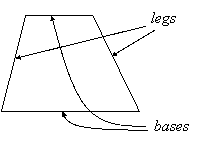
DEFINITION:    An isosceles trapezoid is a trapezoid in which the legs are congruent.

Square, Rhombus, Kite

Other special quadrilaterals are the square, the rhombus, and the kite:

DEFINITION:      A square is a rectangle in which all four sides are congruent.

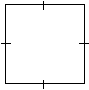
 DEFINITION:      A rhombus is a parallelogram in which all four sides are congruent.

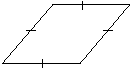
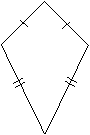
 DEFINITION:      A kite is a quadrilateral in which two pairs of adjacent sides are congruent.

Inheritance of Properties

Some of these special quadrilaterals include others. In this sense, they "inherit" their properties.  For example, all rectangles are parallelograms, and all squares are rectangles (and therefore also parallelograms).  The following flowchart should help keep this straight.  Each object is also an object it is connected to above and has all the properties of the quadrilateral above:

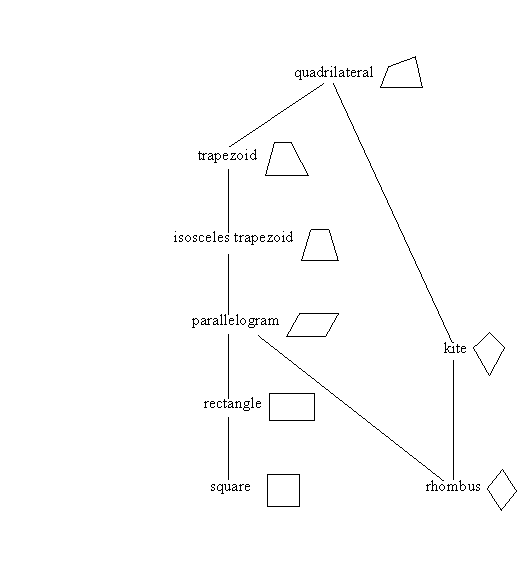
For example, a rhombus is both a kite and a parallelogram, and since a parallelogram is an isosceles trapezoid, a rhombus is also an isosceles trapezoid, a trapezoid, and of course a quadrilateral.

Diagonals of Special Quadrilaterals

As seen from the carpenter's example at the beginning of this lesson, diagonals play an important role in identifying special quadrilaterals.  The theorems about the diagonals of special quadrilaterals are easily proved by identifying congruent triangles formed.  Rather than go through all these theorems and their proofs, we will list the main results in a table:

The X's in this table specify that the diagonals of the given quadrilateral have the indicated properties, and conversely if the diagonals have the indicated properties then the quadrilateral is of the specified type.  For example, if the diagonals of a quadrilateral are congruent and bisect each other, then that quadrilateral is a rectangle.  The "special kite" is a kite in which the diagonals are congruent:

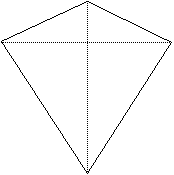
Results about quadrilaterals are usually proved by splitting the quadrilateral into triangles and using SSS, SAS or ASA to prove the triangles congruent.  For example, to prove that opposite sides of a parallelogram are congruent, we would draw a single diagonal and then prove the two resulting triangles are congruent by ASA, from which the result follows since the sides of the parallelogram are corresponding parts of the congruent triangles.

There is an important theorem about the midsegment of a trapezoid that should be discussed separately.  Recall the following result about a midsegment of a triangle:

A midsegment of a triangle is a segment joining the midpoints of two sides.  It is parallel to the third side and half its length:

From this theorem, we can derive a similar result for trapezoids.   The midsegment of a trapezoid is the segment joining the midpoints of its legs:

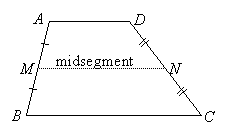
Since parallel lines cut transversals (which are the legs of the trapezoid) into proportional segments, it follows that the midsegment is parallel to the bases.  To see how the length of the midsegment is related to the lengths of the bases,  draw segment  parallel to leg , intersecting  at Q. 

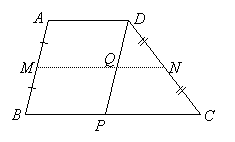
Then  is a midsegment of , so . But ADPB and ADQM are parallelograms, so MQ = AD and BP = AD, and since MN = MQ + QN and BC = BP + PC, we have:  MN = AD + QN, and BC = AD + 2QN.  That is, the lengths AD, MN and BC are in an arithmetic progression, which means they are equally spaced on the number line.  Another way to say this is:  MN is half-way between AD and BC.  We also call MN the average of AD and BC, and from algebra you recall that we can find an average of two numbers by adding them and dividing by 2.

EXAMPLE:

Find the length of the midsegment in the trapezoid on the right.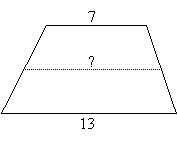

 SOLUTION:     One way to solve this is plot 7 and 13 on the number-line and find the number half-way between them:

The midsegment is 10 units long.

 Another way is to add 7 and 13, and divide by 2:  midsegment = .