Theorems about Perpendicular Lines

Another important concept is perpendicular.  By definition, two lines are perpendicular if they intersect at right angles.  That is, two perpendicular lines form 4 right angles.  Segments and rays can also be perpendicular.  This means they intersect in at least one point, and the two lines containing them are perpendicular.

We use perpendicular segments to measure the distance from a point to a line, a point to a plane, or the distance between two parallel lines or planes.  The ties of a railroad track are perpendicular to the rails and of the same length.  This common length is the distance between the rails.  (If parallel lines exist, then railroad tracks in space can go on forever.)

There are three theorems about perpendicular lines that you should know.  We will not attempt to prove them here, but if you think about them they should be rather obvious:

Theorem 1:  Given a line and a point not on that line, there is one and only one line through the given point that is perpendicular to the given line.

 

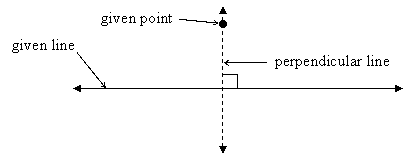
We can use this fact to define the distance from a point to a line:  That distance is the length of a segment perpendicular to the line with the given point as one of its endpoints and the other endpoint on the line.  In fact, a similar notion holds in 3 dimensions.  If we have a plane and a point not on that plane, then there is only one line through the point perpendicular to the plane, and the length of the segment determined by that point and the intersection of the perpendicular line with the plane is defined as the distance from the point to the plane.

Theorem 2:  If two coplanar lines are perpendicular to a third line, then they are parallel to each other:

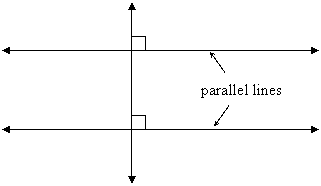
This is a special case of the more general result that when two coplanar lines are cut by a transversal and corresponding angles are equal, then the lines are parallel.  In this case, the corresponding angles are right angles.

Theorem 3  (the Perpendicular Bisector Theorem):

Any point on the perpendicular bisector of a segment is equidistant from the endpoints of that segment, and conversely:

 

 

The perpendicular bisector of a segment is a line that goes through the midpoint of the segment and is perpendicular to it.  This theorem tells us we can think of a perpendicular bisector as the set of all points that are equidistant from the endpoints of the segment.

toc | return to top | previous page