(that is, they will be supplementary). Such angles are called same-side interior angles:Parallel and Perpendicular Lines
Two lines are said to be parallel when they are contained in the same plane and do not intersect. This is the definition. That parallel lines exist is an assumption (postulate) of Euclidean geometry:
Parallel Postulate: Given a line and a point not on that line, there is one and only one line through the given point parallel to the given line.
Parallel lines are like the rails of a train track, and you might think of defining them this way, as lines that are the same distance apart everywhere. The problem with this kind of definition is it assumes both tracks are straight. Though this seems an obvious possibility, when you go into the vast universe it is not that obvious. Parallel lines puzzled the best mathematicians for centuries until it was realized that we must assume they exist (you can't prove they exist from simpler postulates). The problem with parallel lines lies in the notion that the lines have infinite extent.
Euclid used a somewhat different parallel postulate in trying to avoid the notion of the infinite. He observed that when two parallel lines are intersected by a third line, called a transversal, then if you measure two angles formed by these three lines, on the same side of the transversal and between the parallels, they will add to (that is, they will be supplementary). Such angles are called same-side interior angles:
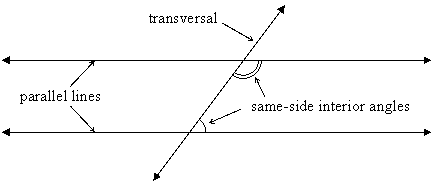
For his parallel postulate, Euclid used the contrapositive of this: If two coplanar lines are intersected by a transversal and a pair of same-side interior angles do not add to 
, then they intersect on the side where the sum is less than 
. You can see that this is a rather awkward statement and more difficult to understand than the parallel postulate we use today (which is sometimes called the Playfair Postulate, named after the dude who thought it up).
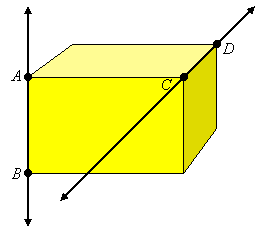
It is important in the definition that we mention that the lines are in the same plane (they are coplanar). In space, two non-intersecting lines can be skew. Skew lines extend in different directions and do not intersect, as lines 
and 
in the following picture of a 3-dimensional box:
The concept of a transversal is very important when studying parallel lines. Pairs of angles formed by the three lines are either congruent or supplementary, depending on which pair is named. Such pairs are given the following special names:
same-side interior
same-side exterior
alternate interior
alternate exterior
corresponding
The following pictures show what these terms mean:
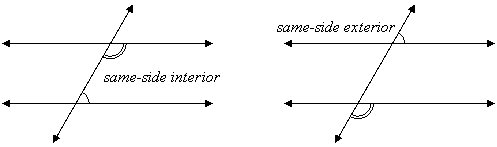
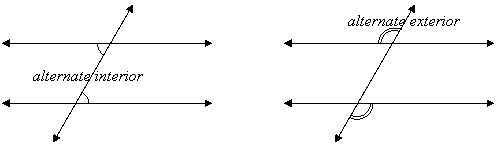
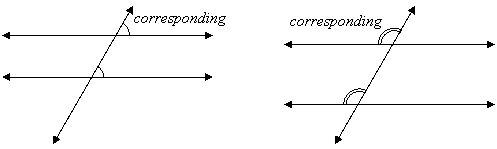
When the two lines (other than the transversal) are parallel, it can be seen that same-side angles are supplementary (they add up to 180o), and when the angles are alternate or corresponding they are congruent (equal). The converses of these are also true. For example, if a transversal cuts two coplanar lines and the alternate interior angles are equal, then the lines must be parallel.
Another important concept is perpendicular. By definition, two lines are perpendicular if they intersect at right angles. That is, two perpendicular lines form 4 right angles. Segments and rays can also be perpendicular. This means they intersect in at least one point, and the two lines containing them are perpendicular.
We use perpendicular segments to measure the distance from a point to a line, a point to a plane, or the distance between two parallel lines or planes. The ties of a railroad track are perpendicular to the rails and of the same length. This common length is the distance between the rails. (If parallel lines exist, then railroad tracks in space can go on forever.)
There are three theorems about perpendicular lines that you should know. We will not attempt to prove them here, but if you think about them they should be rather obvious:
Theorem 1: Given a line and a point not on that line, there is one and only one line through the given point that is perpendicular to the given line.
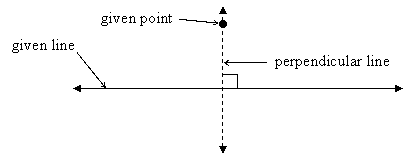
We can use this fact to define the distance from a point to a line: That distance is the length of a segment perpendicular to the line with the given point as one of its endpoints and the other endpoint on the line. In fact, a similar notion holds in 3 dimensions. If we have a plane and a point not on that plane, then there is only one line through the point perpendicular to the plane, and the length of the segment determined by that point and the intersection of the perpendicular line with the plane is defined as the distance from the point to the plane.
Theorem 2: If two coplanar lines are perpendicular to a third line, then they are parallel to each other:
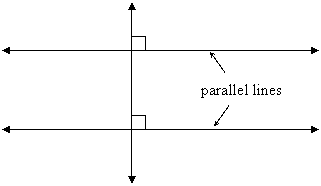
This is a special case of the more general result that when two coplanar lines are cut by a transversal and corresponding angles are equal, then the lines are parallel. In this case, the corresponding angles are right angles.
Theorem 3 (the Perpendicular Bisector Theorem):
Any point on the perpendicular bisector of a segment is equidistant from the endpoints of that segment, and conversely:
The perpendicular bisector of a segment is a line that goes through the midpoint of the segment and is perpendicular to it. This theorem tells us we can think of a perpendicular bisector as the set of all points that are equidistant from the endpoints of the segment.
When you're done, click here to go back to the main Lesson 5 page.