Right Triangles

The main results about right triangles are these:

The Pythagorean Theorem:  c² = a² + b²

The altitude to the hypotenuse forms three similar triangles:

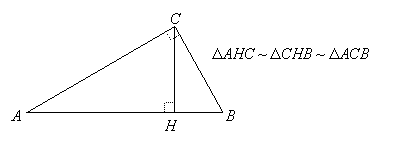In setting up similarity proportions, it is helpful to think in terms of "long leg," "short leg," and "hypotenuse" for each triangle.  For example, in triangles ACB and HCB, the long legs of each correspond and the short legs of each correspond, so the following ratio would be correct (ratio of long legs = ratio of short legs):

EXAMPLE 5:  Find MP:

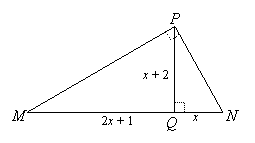SOLUTION:  The left and right triangles are similar. 

PQ is the short leg of the left triangle (triangle MQP) and corresponds to QN, which is the short leg of the right triangle (triangle NQP). 

MQ is the long leg of the left triangle and corresponds to PQ, which is the long leg of the right triangle. 

The ratios of short legs and long legs of these triangles are equal, so

We cross-multiply and solve:

(x + 2)(x + 2) = x(2x + 1)

x² + 4x + 4 = 2x² + x

0 = x² – 3x – 4

0 = (x – 4)(x + 1)

So x = 4 or –1.

But x cannot be negative since it is a side-length of triangle NQP.

Now, looking at triangle MQP, MQ = 2(4) + 1 = 9, and QP = 4 + 2 = 6. 

MP is the hypotenuse, so we can use the Pythagorean Theorem to find it:

MP² = 9² + 6² = 81 + 36 = 117

Therefore,

toc | return to top | previous page