Parallel Lines

When several parallel lines are cut by transversals, the resulting segments are proportional:

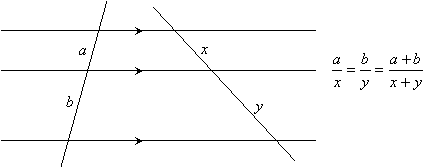EXAMPLE 3: 

Given:  AP = 5x + 1,  PN = x + 1, NB = 12, CM = 15, MD = 3x

Find AB:

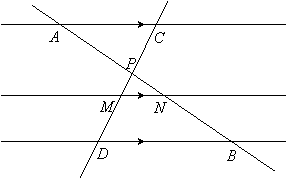SOLUTION:  Think of placing a 4^th parallel line through point P and then move transversal CD to the right so it is clear which segments correspond:

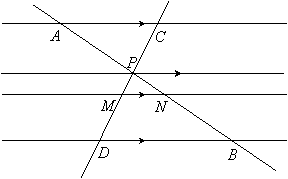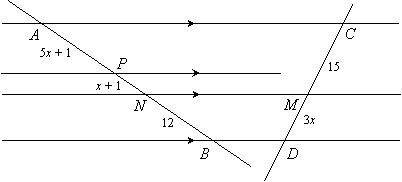Now it is clear that AN corresponds to CM and NB corresponds to MD.  Since AN = AP + PN, we know AN = 6x + 2.  Therefore we can use the following proportion to solve for x:

Cross-multiplying gives us a quadratic equation which we solve:

3x(6x + 2) = 12 ^. 15

18x² + 6x = 180

18x² + 6x – 180  =  0

We can factor a 6 on the left, and then factor by FOIL:

6(3x² + x – 30) = 0

6(3x + 10)(x – 3) = 0

Since x cannot be negative (because 3x is the length of one of the segments), the only solution that makes sense is x = 3.

Now we can find the length of segment AB:

AB = (5x + 1) + (x + 1) + 12 = 16 + 4 + 12 = 32

toc | return to top | previous page | next page