Finding Segment Lengths
Segment Addition
When a segment is split by points between its endpoints, the lengths of the subsegments add to the length of the segment.
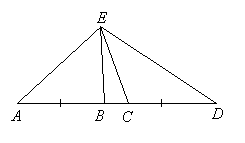
EXAMPLE 1: In the figure below, AB = CD, AC = 3x + 18, and BD = 3 – 2x. Find AB.
 |
SOLUTION: Since AC = AB + BC and BD = BC + CD = BC + AB, it follows that these segments are equal in length.
Therefore 3x + 18 = 3 – 2x.
Solving: 5x + 18 = 3, 5x = –15, x = –3.
So AB = 3(–3) + 18 = 9
Similar Figures
When two figures are similar, the ratios of corresponding sides will be equal.
EXAMPLE 2:
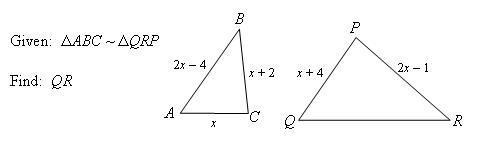
SOLUTION: AC corresponds to QP and BC corresponds to RP, so we can use the following proportion:
![]()
We can solve this by cross-multiplying:
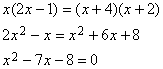
Now factor:
![]()
This has solutions x = 8 and x = –1.
Since x is a side of a triangle, it cannot be negative, so the only meaningful solution is x = 8.
Now side QR corresponds to side AB. Since AB = 2(8) – 4 = 12, we can use a ratio to find QR.
To get the ratio, we also need side QP since that corresponds to AC and we know AC = 8.
QP = 8 + 4 = 12. Now we can find QR:
![]()
Cross-multiplying: 8QR = 144, so QR = 18
Parallel Lines
When several parallel lines are cut by transversals, the resulting segments are proportional:
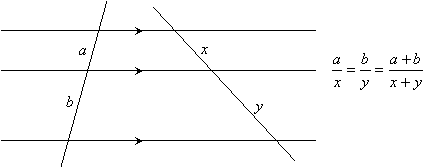 |
EXAMPLE 3:
Given: AP = 5x + 1, PN = x + 1, NB = 12, CM = 15, MD = 3x
Find AB:
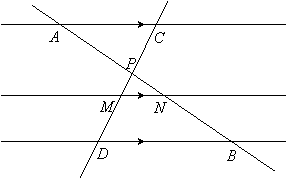 |
SOLUTION: Think of placing a 4th parallel line through point P and then move transversal CD to the right so it is clear which segments correspond:
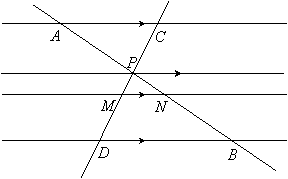 |
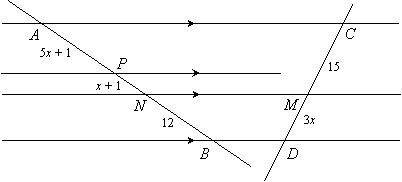 |
Now it is clear that AN corresponds to CM and NB corresponds to MD. Since AN = AP + PN, we know AN = 6x + 2. Therefore we can use the following proportion to solve for x:
![]()
Cross-multiplying gives us a quadratic equation which we solve:
3x(6x + 2) = 12 . 15
18x2 + 6x = 180
18x2 + 6x – 180 = 0
We can factor a 6 on the left, and then factor by FOIL:
6(3x2 + x – 30) = 0
6(3x + 10)(x – 3) = 0
Since x cannot be negative (because 3x is the length of one of the segments), the only solution that makes sense is x = 3.
Now we can find the length of segment AB:
AB = (5x + 1) + (x + 1) + 12 = 16 + 4 + 12 = 32
The Midsegment of a Trapezoid
The midsegment of a trapezoid connects the midpoints of the non-parallel sides and is parallel to the bases (parallel sides). Its length is the average of the base-lengths.
EXAMPLE 4: Find the length of CD:
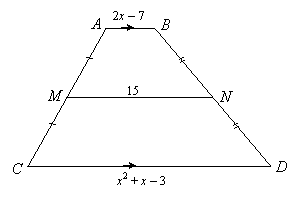 |
SOLUTION: 15 is the average of AB and CD, so
![]()
We can multiply both sides of this equation by 2 and combine like terms on the left to get:
![]()
So:
![]()
So x = –8 or x = 5
But x cannot be –8 since that would make 2x – 7 negative.
Therefore, CD = x2 + x – 3 = 25 + 5 – 3 = 27
Right Triangles
The main results about right triangles are these:
The Pythagorean Theorem: c2 = a2 + b2
 |
The altitude to the hypotenuse forms three similar triangles:
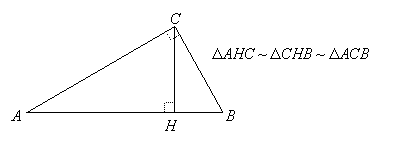 |
In setting up similarity proportions, it is helpful to think in terms of "long leg," "short leg," and "hypotenuse" for each triangle. For example, in triangles ACB and HCB, the long legs of each correspond and the short legs of each correspond, so the following ratio would be correct (ratio of long legs = ratio of short legs):
![]()
EXAMPLE 5: Find MP:
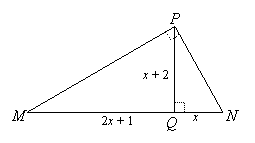 |
SOLUTION: The left and right triangles are similar.
PQ is the short leg of the left triangle (triangle MQP) and corresponds to QN, which is the short leg of the right triangle (triangle NQP).
MQ is the long leg of the left triangle and corresponds to PQ, which is the long leg of the right triangle.
The ratios of short legs and long legs of these triangles are equal, so
![]()
We cross-multiply and solve:
(x + 2)(x + 2) = x(2x + 1)
x2 + 4x + 4 = 2x2 + x
0 = x2 – 3x – 4
0 = (x – 4)(x + 1)
So x = 4 or –1.
But x cannot be negative since it is a side-length of triangle NQP.
Now, looking at triangle MQP, MQ = 2(4) + 1 = 9, and QP = 4 + 2 = 6.
MP is the hypotenuse, so we can use the Pythagorean Theorem to find it:
MP2 = 92 + 62 = 81 + 36 = 117
Therefore,
![]()
Return to Lesson 3