Example 4:

Find θ to the nearest degree in this triangle:

 

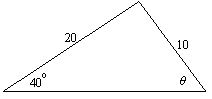
Solution:

Again we have an SSA case, but this time it appears θ is less than 90^o, so we should be able to directly apply the Law of Sines:

If we try to find the inverse sine of 1.285575 using a calculator, we would discover it gives an error.  This is because the sine of an angle (any angle) is never greater than 1 (remember?  the general definition of sin θ is y/r, and y can never be greater than r since it is a coordinate of a point on the circle of radius r centered at the origin).

If we were to try and construct this triangle, we would see it is impossible, since a right triangle with hypotenuse 20 would have its leg opposite the 40^o angle equal to 12.86 units:

So the given triangle cannot exist.

toc | return to top | previous page | next page