Example 3:

Find the value of θ to the nearest degree:

 

Solution:

If we directly apply the Law of Sines, we have:

and we might then conclude:

However, the diagram clearly shows θ is greater than 90o, so something fishy is happening here.

Looking more closely at the triangle, we are given two sides and an angle, but the angle is not included between the two sides.  This is an SSA case, and there is no theorem that guarantees such a triangle is unique.  In fact, the θ = 51o is the answer to this problem instead:

To understand what is happening here, we construct a right triangle with an angle of 34o and hypotenuse 25 units.  The length of the leg opposite the 34o angle turns out to be 13.98 units:

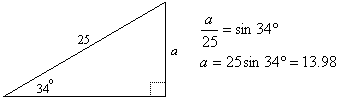
Now the side opposite the 34o angle in the given triangle is longer than 13.98.  If we were to try and construct that triangle, we would find there are two points where it could intersect the bottom side:

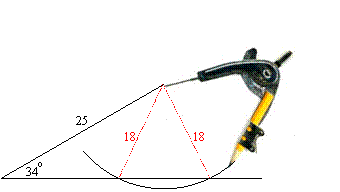
In view of this we have two possible triangles:

Now we can see that the θ we wanted is 180o – 51o = 129o.  In fact, the sine of 129o is the same as the sine of 51o, as both have the same reference angle (51o), and the sine of an angle in the second quadrant is positive.


toc | return to top | previous page | next page