The Law of Sines

An Area Formula

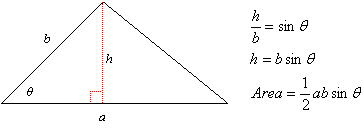
Suppose you know two sides and the included angle of a triangle:

To find its area, you could drop a perpendicular from the top vertex to the bottom side and use trig to find it length.  This is an altitude, so you could then find the area:

If we call the lengths of the given sides a and b, and the included angle θ, then we can use this reasoning to find a formula:

Example 1:

Two sides of a triangle measure 10 cm and 12 cm, and the angle between them measures 130^o.  What is the area of that triangle?

Solution:

The Law of Sines

If we label our triangle in the usual way, then we can give 3 different formulas for the area, depending on which two sides and the included angle are used:

Since these three formulas give the same area, the expressions on the right are all equal, so each of the following must be true:

These simplify to:

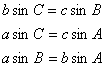
The can be rewritten as ratios:

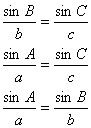
or more compactly as:

The following examples illustrate the use of this Law of Sines for finding missing parts of triangles.

Example 2:

Find the length of the side marked x:

Solution:

We must first find the missing angle.  Its measure is 180^o – 34^o – 95^o = 51^o.  Then we can apply the Law of Sines to find x since it is opposite the 51^o angle:

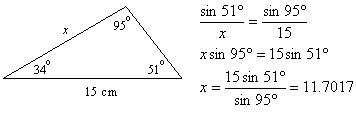
So the side labeled x is about 11.7 cm long.

Example 3:

Find the value of θ to the nearest degree:

Solution:

If we directly apply the Law of Sines, we have:

and we might then conclude:

However, the diagram clearly shows θ is greater than 90^o, so something fishy is happening here.

Looking more closely at the triangle, we are given two sides and an angle, but the angle is not included between the two sides.  This is an SSA case, and there is no theorem that guarantees such a triangle is unique.  In fact, the θ = 51^o is the answer to this problem instead:

To understand what is happening here, we construct a right triangle with an angle of 34^o and hypotenuse 25 units.  The length of the leg opposite the 34^o angle turns out to be 13.98 units:

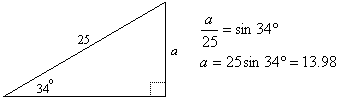
Now the side opposite the 34^o angle in the given triangle is longer than 13.98.  If we were to try and construct that triangle, we would find there are two points where it could intersect the bottom side:

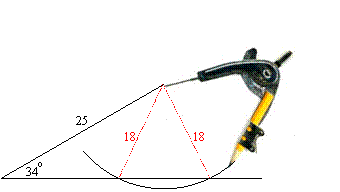
In view of this we have two possible triangles:

Now we can see that the θ we wanted is 180^o – 51^o = 129^o.  In fact, the sine of 129^o is the same as the sine of 51^o, as both have the same reference angle (51^o), and the sine of an angle in the second quadrant is positive.

Example 4:

Find θ to the nearest degree in this triangle:

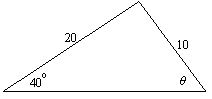
Solution:

Again we have an SSA case, but this time it appears θ is less than 90^o, so we should be able to directly apply the Law of Sines:

If we try to find the inverse sine of 1.285575 using a calculator, we would discover it gives an error.  This is because the sine of an angle (any angle) is never greater than 1 (remember?  the general definition of sin θ is y/r, and y can never be greater than r since it is a coordinate of a point on the circle off radius r centered at the origin).

If we were to try and construct this triangle, we would see it is impossible, since a right triangle with hypotenuse 20 would have its leg opposite the 40^o angle equal to 12.86 units:

So the given triangle cannot exist.

Example 5:

Find θ to the nearest degree in this triangle:

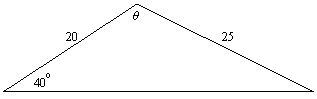
Solution:

Again we have an SSA case, but we cannot find θ directly since the side opposite it is also unknown.  Therefore we will find the angle opposite the side of length 20 and then use the fact that the angles in a triangle add to 180^o:

Since the side opposite the 40o angle is greater than the adjacent side, there can only be one such triangle, and α is less than 90^o so the Law of Sines gives its value directly:

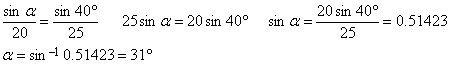
Return to Lesson 16