Proof:

The proof of this theorem is much the same as the proof of the previous theorem.  We need to establish that any point on the original figure gets rotated through an angle twice the angle between the intersecting lines.  Let d be the angle between the intersecting lines, let P be a point on the original figure, and let x be the angle from P to the first line as in the figure:

 

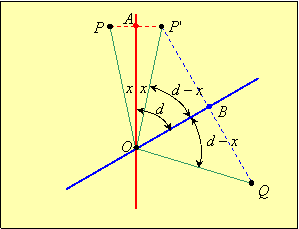
In the figure, O is the point of intersection of the two reflection lines, A is the point of intersection of the perpendicular through P with the first reflection line, and B is the point of intersection of the perpendicular from the image P' in the second reflection line.  Triangles POA and P'OA are congruent right triangles (by SAS) as are triangles P'OB and QOB.  So if angle POA is x, then so is angle P'OA.  Therefore angle P'OB measures d – x since angle AOB is d.  But angle AOB is congruent to angle P'OB, so it also measures d – x.  Thus angle POQ measures x + x + d – x + d – x = 2d.

toc | return to top | previous page