Isometry Theorems
There is a connection between reflections, translations and rotations.
Theorem 1: When a figure is reflected in two parallel lines, the end result is the same as a translation in the direction perpendicular to the parallel lines and twice the distance between them.
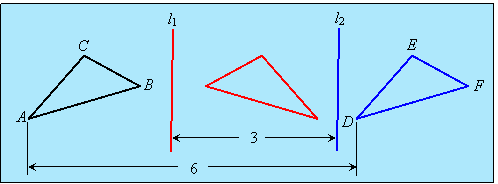
For example, if triangle ABC is reflected in line l1 and the image is reflected in line l2, then the final image (triangle DEF) is a translation of triangle ABC through 6 units:
 |
Proof:
This can be proved by showing any point on the preimage is translated a distance twice that of the distance between the lines:
Suppose the distance between the parallel lines is d, and consider a point P on the preimage. If P is a distance x from l1, then its image P' upon reflection in l1 is a distance x on the other side of l1, and is therefore a distance d – x from l2. When P' is reflected in l2, then its image Q is a distance d – x on the other side of l2. The distance from P to Q is equal to the distance from P to l1 plus the distance from l1 to P' plus the distance from P' to l2 plus the distance from l2 to Q: PQ = x + x + d – x + d – x = 2d.
 |
Theorem 2: When a figure is reflected in two intersecting lines, then the final image is a rotation of the figure about the point of intersection of the reflecting lines through an angle twice the angle between the intersecting lines.
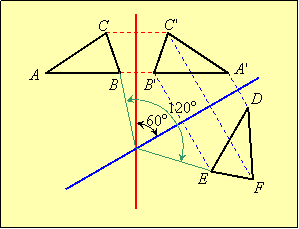 |
Proof:
The proof of this theorem is much the same as the proof of the previous theorem. We need to establish that any point on the original figure gets rotated through an angle twice the angle between the intersecting lines. Let d be the angle between the intersecting lines, let P be a point on the original figure, and let x be the angle from P to the first line as in the figure:
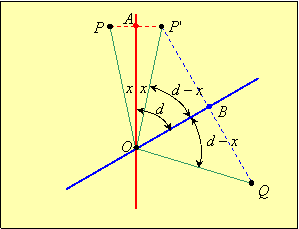
In the figure, O is the point of intersection of the two reflection lines, A is the point of intersection of the perpendicular through P with the first reflection line, and B is the point of intersection of the perpendicular from the image P' in the second reflection line. Triangles POA and P'OA are congruent right triangles (by SAS) as are triangles P'OB and QOB. So if angle POA is x, then so is angle P'OA. Therefore angle P'OB measures d – x since angle AOB is d. But angle AOB is congruent to angle P'OB, so it also measures d – x. Thus angle POQ measures x + x + d – x + d – x = 2d.
Return to Lesson 4