More on Segments

Lines and rays go on forever.  We sometimes express this by saying they have "infinite length."  Segments, on the other hand, have fixed endpoints, so they can be measured.  The length of a segment can be expressed in any of the standard units, such as inches, centimeters, feet, meters, miles, etc.  When we label segments, we place a bar over the letters of their endpoints, like this: .  If we do not place the bar above the letters of the endpoints, the label represents the length of the segment.  Thus, AB represents the length of : 

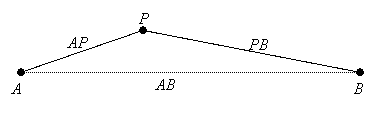
Segments can be cut into smaller segments, and the lengths of these smaller segments add to the length of the whole segment.  For example, if P is a point between A and B, then P splits  into the two segments,  and , and AB = AP + PB:

A postulate is implied by the above figure.  It is sometimes called the Segment Addition Postulate:

Segment Addition Postulate:    If P is between A and B then AB = AP + PB, and conversely.

The "and conversely" part of this postulate means, if AB = AP + PB then P is between A and B.  It implies that a point can be "between" two other points only when the three points are collinear.

Everybody knows that "the shortest distance between two points is a line."  More precisely, the shortest distance between two points is the length of the segment joining those points.  This is another postulate in geometry, and helps clarify the notion that lines and segments are "straight."  When combined with the Segment Additions Postulate, it implies the following theorem:

Triangle Inequality:    If points A, B and P are noncollinear, then AB < AP + PB.

If the three points are collinear, then it is still possible that AB < AP + BP.  This would happen when P is not between A and B, and follows from algebra.  For example, if B is between A and P, then AP = AB + BP,

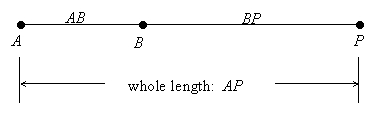
and so AB = AP – BP.  Since distances are positive, AB < AP.

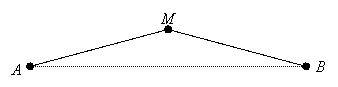
We can also talk about the midpoint of a segment.  That is the point halfway between the endpoints.  More precisely, we can define midpoint as follows:

Definition:  M is the midpoint of  if M is between A and B, and AM = MB.

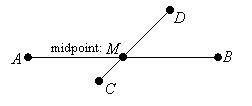
In this definition we must specify that M is between A and B, as the following example illustrates:

 Example:      AM = MB, but M is not between A and B because it is not on the same line as A and B:

Another term that is sometimes used when something is cut in half is the word bisect.  The midpoint of a segment bisects it.  Lines, rays and other segments can also bisect a given segment.  In the following diagram, segment  bisects segment  at point M:

toc | return to top | previous page | next page