Segments, Rays and Angles
In geometry, a line is straight and goes on forever. To indicate that a line goes on forever, we usually draw lines with arrows on both ends, like this:
Lines are sometimes labeled by indicating two points on them and placing a double arrow over the names of the points (which are capital letters). For example, the line that goes through points A and B might be labeled as 
:
If we choose a point on a given line this divides the line into two pieces or "halves." Each half is called a ray. More precisely, a ray consists of a point on a line, called its vertex, and all points on one side (or half) of that line. A ray goes on forever, but only in one direction. We draw rays with an arrow on one side only, like this:
Rays are labeled by specifying the vertex and some other point on it, and placing an arrow over these letters. Ray 
would look like this:
If we choose two distinct points on a line, the line is split into three pieces. The piece that consists of those two points and all the points between them is called a segment. Segments do not go on forever, so we do not put arrows on their ends. The endpoints of segments are called its vertices, and we label segments by specifying the endpoints and placing a line without arrows over these letters. Segment 
would look like this:
Recall that an angle is made of two rays with a common vertex. The rays are the sides of the angle, and they go on forever. This means it doesn't matter how long you draw those rays, so the following two angles are really the same size even though they look different:
Angles are sometimes labeled using letters of three points on them, the vertex and one on each side of the angle. The vertex-letter is always the middle letter. There are two names we could give the following angle. It could be labeled 
or 
:
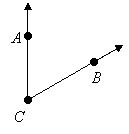
When there is no confusion, we can also use just the vertex to name an angle. In the above case, we could name the angle as 
.
The size of an angle depends on how much its sides slant away from each other and is usually measured in degrees. Degrees are determined by drawing a circle centered at the vertex of the angle, placing 360 equally-spaced marks on the circle, and counting the number of marks on the shorter arc of the circle between the sides. Such a circle is called a protractor. Since the shorter arc is always used, protractors are usually constructed as semicircles (half circles) instead of full circles, and an angle cannot contain more than 180 degrees.
Here we review the definitions of certain special angles and properties of angles.
Definition: When the rays are the two halves of a line (they point in opposite directions), the angle is called a straight angle:
A straight angle measures 180o.
Definition: When the sides of an angle are perpendicular, the angle is called a right angle:
A right angle measures 90o.
Definition: If the measure of the angle is less than 90o the angle is called an acute angle:
Definition: if the measure is more than 90o the angle is called an obtuse angle:
Definition: When a point is the vertex of the angle or on a side of the angle, it is said to be on the angle.
Definition: A point is interior to an angle if it lies on some segment with endpoints on the sides of the angle. An object such as a ray or segment is interior to an angle if all its points other than its vertex or vertices are interior to that angle (a vertex can be interior or on the angle, as long as the other points are interior).
For example, point P is interior to 
because it is on segment 
, where D and E are points on the sides of the angle, and the whole segment 
is also interior:
Definition: A point, ray, or segment is exterior to an angle if it is not interior to that angle.
Lines and rays go on forever. We sometimes express this by saying they have "infinite length." Segments, on the other hand, have fixed endpoints, so they can be measured. The length of a segment can be expressed in any of the standard units, such as inches, centimeters, feet, meters, miles, etc. When we label segments, we place a bar over the letters of their endpoints, like this: 
. If we do not place the bar above the letters of the endpoints, the label represents the length of the segment. Thus, AB represents the length of 
:
Segments can be cut into smaller segments, and the lengths of these smaller segments add to the length of the whole segment. For example, if P is a point between A and B, then P splits 
into the two segments, 
and 
, and AB = AP + PB:
A postulate is implied by the above figure. It is sometimes called the Segment Addition Postulate:
Segment Addition Postulate: If P is between A and B then AB = AP + PB, and conversely.
The "and conversely" part of this postulate means, if AB = AP + PB then P is between A and B. It implies that a point can be "between" two other points only when the three points are collinear.
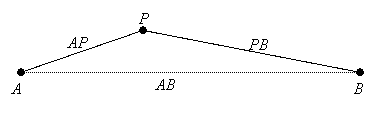
Everybody knows that "the shortest distance between two points is a line." More precisely, the shortest distance between two points is the length of the segment joining those points. This is another postulate in geometry, and helps clarify the notion that lines and segments are "straight." When combined with the Segment Additions Postulate, it implies the following theorem:
Triangle Inequality: If points A, B and P are noncollinear, then AB < AP + PB.
If the three points are collinear, then it is still possible that AB < AP + BP. This would happen when P is not between A and B, and follows from algebra. For example, if B is between A and P, then AP = AB + BP,
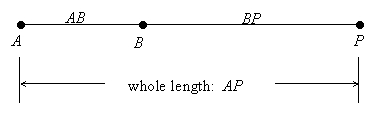
and so AB = AP – BP. Since distances are positive, AB < AP.
We can also talk about the midpoint of a segment. That is the point halfway between the endpoints. More precisely, we can define midpoint as follows:
Definition: M is the midpoint of 
if M is between A and B, and AM = MB.
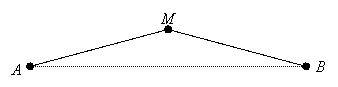
In this definition we must specify that M is between A and B, as the following example illustrates:
Example: AM = MB, but M is not between A and B because it is not on the same line as A and B:
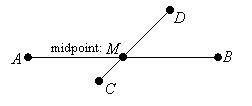
Another term that is sometimes used when something is cut in half is the word bisect. The midpoint of a segment bisects it. Lines, rays and other segments can also bisect a given segment. In the following diagram, segment 
bisects segment 
at point M:
When two segments have the same length we say they are "equal." When we want to distinguish between a segment and its length, we use a bar over its endpoints for the physical object and no bar for the length. In geometry, we say two physical objects are congruent when they have the same measure, and we use an equals-sign with a "tilde" over it:
As we learned before, angles are notated with a slanting L. If they have the same measure (degrees), we should say they are congruent and again use an equals-sign with a tilde over it. If we want to focus on their measures, then we need another notation. The standard is to place an "m" before the name of the angle:
As with segments, angles can also be bisected. The bisector of an angle is a ray that cuts that angle into two equal angles:
The bisector of an angle is a ray interior to the angle that cuts it in half. This is similar to saying that the midpoint of a segment is a point on that segment (or "between" its endpoints) that cuts it into two equal segments. Thus, a precise definition of angle bisector is:
Definition: Ray 
is the bisector of 
if it is interior to the angle and 
:
As with the Segment Addition Postulate for segments, we have an Angle Addition Postulate:
Angle Addition Postulate: If 
is interior to 
, then 
:
In this case, 
and 
are adjacent angles. (Adjacent are two angles that share a common ray.) When adjacent angles are equal, the common ray is the bisector of the larger angle. That is, the bisector of an angle is a ray that spits it into two equal pieces.
When adjacent angles add to 
, the two non-common rays form a straight angle, and the two angles are called a linear pair:
The word supplementary is given when two angles add to 180o. This word is less specific than linear pair in that the angles do not have to be adjacent. Their measures just have to add to 180o. These angles are supplementary, but not a linear pair:
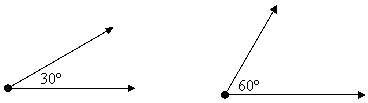
When the non-common rays of adjacent angles are perpendicular, their measures add to 90o:
In general, any two angles that add to 90o are called complementary. They need not be adjacent:
When you're ready, click here to return to the main Lesson 5 page.