Lines that Have a Simple Pattern

An equation of a line is a statement about every point on the line, using the variables x and y for the coordinates.  That is, it is an equation in x and y with points on the line as its solutions.  Such an equation does not have to have both x and y.  For example, the equation 2x + 7 = 1 is the equation of some line even though it does not contain the variable y.

The equations of some lines can be discovered using inductive reasoning (looking for patterns).  This is true of horizontal and vertical lines, as well some slanting lines.  The following examples illustrate this.

Example 1: 

Find an equation of the vertical line:

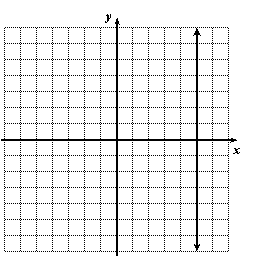
Solution: Pick some points on the line (at least 3) and list their coordinates. Then look for an obvious pattern:

 

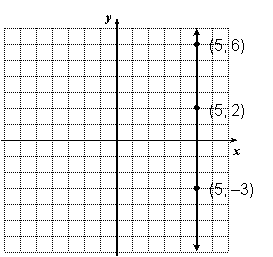
In every case the x-coordinate is 5.  So the equation is simply x = 5.

Example 2: 

Find an equation of the horizontal line.

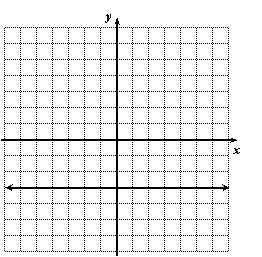
Solution: 

Again pick some points on the line and list their coordinates.

In every case the y-coordinate is –3.  So the equation is simply y = –3.

Example 3: 

Find an equation of the 45^o line:

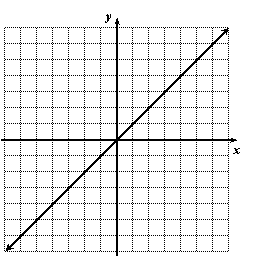
Solution: 

Pick some points (at least 3) on the line and list their coordinates.

In every case the x- and y-coordinates are equal.  So we could write the equation as x = y or as y = x.  Any equivalent form will do.

Example 4: 

Find an equation this line:

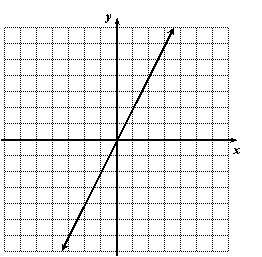
Solution: 

Pick some points (at least 3) on the line and list their coordinates.

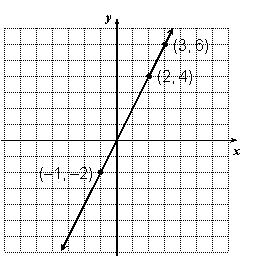
You have to think about this.  The pattern is that the y-coordinate of each point is twice its x-coordinate.  You could look at a couple more points just to be sure.  In any case, we can write the equation as y = 2x.

In the last example, the 2 in front of the x is the slope of the line.  On the next page we will see that slope helps us find an equation of a slanting line.

toc | return to top | next page