Equations of Lines
Lines that Have a Simple Pattern
An equation of a line is a statement about every point on the line, using the variables x and y for the coordinates. That is, it is an equation in x and y with points on the line as its solutions. Such an equation does not have to have both x and y. For example, the equation 2x + 7 = 1 is the equation of some line even though it does not contain the variable y.
The equations of some lines can be discovered using inductive reasoning (looking for patterns). This is true of horizontal and vertical lines, as well some slanting lines. The following examples illustrate this.
Example 1:
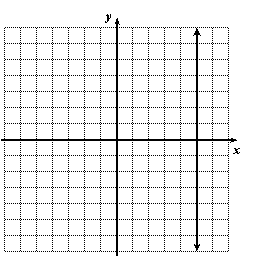
Find an equation of the vertical line:

Solution: Pick some points on the line (at least 3) and list their coordinates. Then look for an obvious pattern:
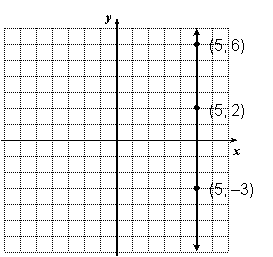
In every case the x-coordinate is 5. So the equation is simply x = 5.
Example 2:
Find an equation of the horizontal line.
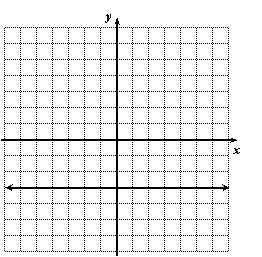
Solution:
Again pick some points on the line and list their coordinates.

In every case the y-coordinate is –3. So the equation is simply y = –3.
Example 3:
Find an equation of the 45o line:
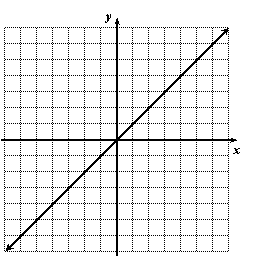
Solution:
Pick some points (at least 3) on the line and list their coordinates.

In every case the x- and y-coordinates are equal. So we could write the equation as x = y or as y = x. Any equivalent form will do.
Example 4:
Find an equation this line:
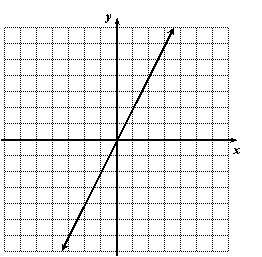
Solution:
Pick some points (at least 3) on the line and list their coordinates.
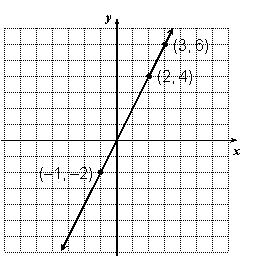
You have to think about this. The pattern is that the y-coordinate of each point is twice its x-coordinate. You could look at a couple more points just to be sure. In any case, we can write the equation as y = 2x.
In the last example, the 2 in front of the x is the slope of the line. On the next page we will see that slope helps us find an equation of a slanting line.
Slanting Lines
If a slanting line passes through the origin, its equation can always be written as y = mx, where m is its slope. For example, an equation of the line below is given in the graph:
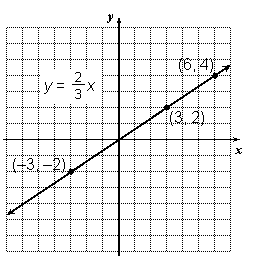
Notice that the slope is 2/3 and each of the points is a solution to the equation. For example, the point (6, 4) is a solution, because 2/3 of 6 is 4.
A slanting line that does not contain the origin can be thought of as a line that has been moved up or down. For example, the following line is the previous line moved down 3 units:
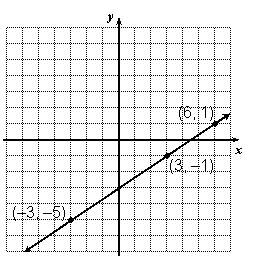
When you move a point up or down, you just change the y-coordinate by adding or subtracting the distance moved. Since this applies to all points on our new line, we must subtract 3 from all the points, and therefore from the equation. So the new equation is:

Now the –3 is the y-intercept. That makes sense, since the point (0, 0) on the original line was moved down 3 units.
In general, an equation of a slanting line with slope m and y-intercept b can be written as:
y = mx + b
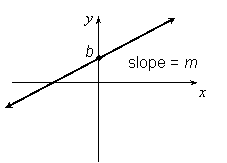
Another example:
The slope of this line is negative since it goes downhill from left to right, and its y-intercept is 5:

Using the Slope Formula
If you know the coordinates of two points on a line and the line is not horizontal or vertical, the slope can always be found by the following formula:
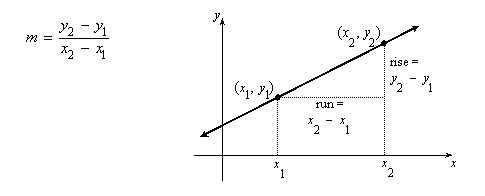
You should realize that is doesn't matter which two points you use to find the slope. If they are on the same line, then any two slope-triangles on the line will give the same fraction for slope when it is reduced. It also follows that parallel lines have the same slope.
If you do not know the y-intercept for a slanting line, the slope formula gives a simple method for finding the equation: Use a "generic point" (x, y) in place of (x2, y2) and equate the slopes. Then "simplify" by multiplying both sides by the denominator.
Example: Find an equation of this line:
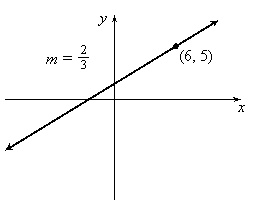
Solution: Using the slope formula with (x, y) in place of (x2, y2) and (6, 5) in place of (x1, y1) we have:
![]()
![]()
![]()
Perpendicular Lines
We already mentioned that parallel lines have the same slope. The animation shows that the slope of a perpendicular line is the opposite reciprocal of the slope of a given line.
Example 1:
![]()
What is the slope of a line perpendicular to that line?
![]()
Example 2:
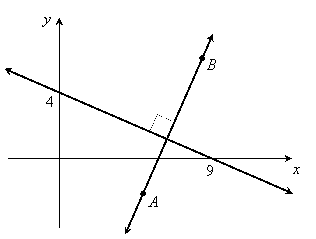
What is the slope of line AB
Solution:
The slope of the line with x-intercept 9 and y-intercept 4 is negative since it goes downhill:
![]()
Since line AB is perpendicular to this line, its slope is the opposite reciprocal:
![]()
Example 3:
A line has equation y = 3x + 2. What is an equation of a line perpendicular to this line, containing the point (4, 5)?
Solution:
The slope of the given line is 2 (m is the number in front of x). As a fraction,
![]()
The perpendicular line's slope is the opposite reciprocal:
![]()
Now use the slope formula with (4, 5) for (x1, y1) and (x, y) for (x2, y2):
![]()
Multiply both sides by (x – 4) and simplify:
![]()
![]()
Click here to return to the main Lesson 7 page.