The Rhombus Problems

A rhombus is a parallelogram in which all four sides are equal.  It is like a "slanted square."  Suppose points A, B, C, and D have coordinates (0, 0), (3, 4), (8, 4), and (5, 0), respectively:

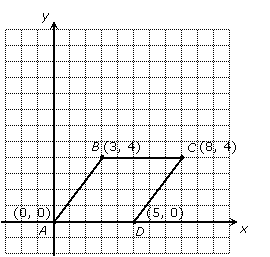
1.   Show that ABCD is a parallelogram.

Solution: 

Sides AD and BC are parallel because they are both horizontal.  Sides AB and CD are parallel if they have the same slope: 

2.   Show that ABCD is a rhombus.

Solution:

We already know it is a parallelogram, so now we must show all sides have the same length.  Since sides AD and BC are horizontal, their lengths are easy to find: 

 

Now we use the distance formula to find the lengths of the other sides:

So all 4 sides have the same length.

 

 

3.   Show that the diagonals of ABCD bisect each other.

Solution:

The easiest way to do this is to show the midpoints of segments AC and BD are the same point:

4.   Show that the diagonals of ABCD are perpendicular.

Solution:

Two lines are perpendicular if their slopes are opposite reciprocals, so we find the slopes of segments AC and BD:

Since 1/2 and –2 are opposite reciprocals, the diagonals are perpendicular.

toc | return to top | previous page