Thie Distance and Midpoint Formulas

The Distance Formula

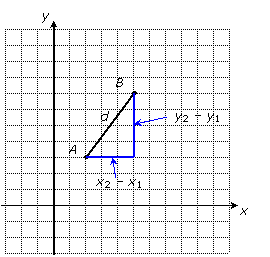
Points A and B have coordinates (2, 3) and (5, 7).  The distance from point A to point B is the length of segment AB.  You can find that distance by drawing a right triangle, finding the lengths of its legs, and then using the Pythagorean Theorem:

Notice that the horizontal leg's length can be found by subtracting the x-coordinates of the points and the vertical leg's length can be found by subtracting the y-coordinates of the points.  In general, if the points have coordinates (x₁, y₁) and (x₂, y₂), then the distance d between them can be found by the Pythagorean Theorem:

or

Example: 

Find the length of segment CD if the coordinates of C are (–4, 7) and the coordinates of D are (2, 3).

Solution:

The Midpoint Formula

On the number line, suppose point A has coordinate 17 and point B has coordinate 25.  What is the coordinate of the midpoint of segment AB?

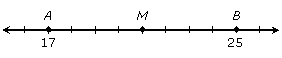
You can see from the diagram that the coordinate is 21.  A shortcut (if you don't want to draw part of a number line) is to find the average of the coordinates:

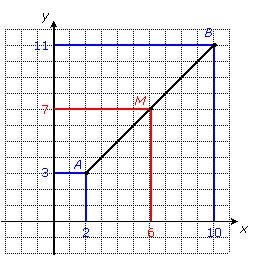
In 2 dimensions, the coordinates of the midpoint of two points is the average of their coordinates.  For example, if the coordinates of A are (2, 3) and the coordinates of B are (10, 11), then the coordinates of the midpoint M of segment AB are (6, 7).

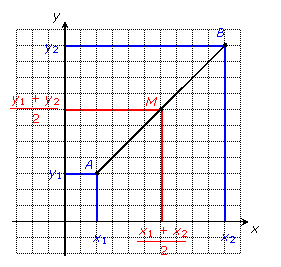
In general, if the points have coordinates (x₁, y₁) and (x₂, y₂), then the midpoint M has coordinates that are the average of these:

An Equation of a Circle

An equation of any shape graphed in the xy-coordinate plane is a statement about all the points on it, using x and y as the coordinates.  If you have a circle of radius 5 centered at the origin, the Pythagorean Theorem tells us something that must be true of all points on the circle:

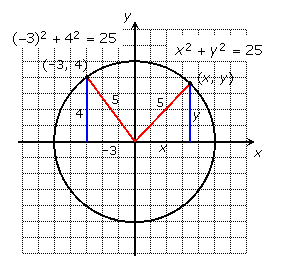
In general, the equation of a circle of radius r centered at the origin is:

The Rhombus Problems

A rhombus is a parallelogram in which all four sides are equal.  It is like a "slanted square."  Suppose points A, B, C, and D have coordinates (0, 0), (3, 4), (8, 4), and (5, 0), respectively:

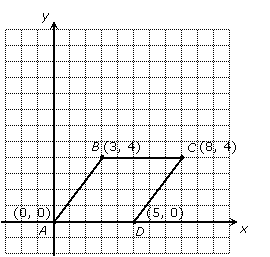
1.   Show that ABCD is a parallelogram.

Solution: 

Sides AD and BC are parallel because they are both horizontal.  Sides AB and CD are parallel if they have the same slope: 

2.   Show that ABCD is a rhombus.

Solution:

We already know it is a parallelogram, so now we must show all sides have the same length.  Since sides AD and BC are horizontal, their lengths are easy to find: 

Now we use the distance formula to find the lengths of the other sides:

So all 4 sides have the same length.

3.   Show that the diagonals of ABCD bisect each other.

Solution:

The easiest way to do this is to show the midpoints of segments AC and BD are the same point:

4.   Show that the diagonals of ABCD are perpendicular.

Solution:

Two lines are perpendicular if their slopes are opposite reciprocals, so we find the slopes of segments AC and BD:

Since 1/2 and –2 are opposite reciprocals, the diagonals are perpendicular.

Click here to return to the main Lesson 8 page.