When a quadrilateral is known to be of certain special type, then additional properties of the diagonals can narrow the type.  The following theorems demonstrate this:

Theorem 5:  If the diagonals of a parallelogram are congruent, then the parallelogram is a rectangle.

Proof:  Let the parallelogram be ABCD with congruent diagonals AC and BD.

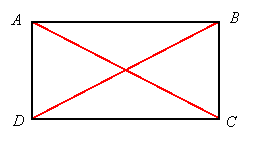
Consider the overlapping triangles ADC and BCD.  Since opposite sides of a parallelogram are congruent, AD = BC.  Since the diagonals of the parallelogram are congruent, AC = BD, and the overlapping triangles have a common side, DC.  Therefore they are congruent by SSS.  So angle ADC and BCD are congruent.  But these are same-side interior angles for parallel lines AD and BC with transversal DC.  Since same-side interior angles add to 180^o, each must be 90^o, so the parallelogram is a rectangle.

This theorem is often used by carpenters to check a door or window to see if it is really rectangular.  First the carpenter measures the opposite sides.  If they are the same length, then he measures the diagonals.  If they too are the same length, then he knows the angles are right angles.

Theorem 6:  If the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus.

Proof: Let the parallelogram be ABCD with perpendicular diagonals AC and BD intersecting at P:

The diagonals of a parallelogram bisect each other, so triangles APB and CPB are congruent by SAS.  Therefore the corresponding parts, sides AB and CB are congruent.  Likewise, triangles BPC and DPC are congruent, so sides BC and DC are congruent, and similarly sides AD and CD are congruent.  So all 4 sides are congruent, which makes the parallelogram a rhombus.

There are other theorems which could be stated, but the main ideas revolve around congruent triangles formed by the diagonals and sides of the quadrilateral.