The diagonals of a quadrilateral can determine whether it is a parallelogram, a rectangle, a rhombus, etc..  We will list and prove the main theorems here.

Theorem 1:  If the diagonals of a quadrilateral bisect each other then the quadrilateral is a parallelogram.

Proof:  Let the quadrilateral be ABCD with diagonals AC and BD intersecting at P:

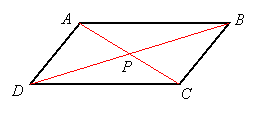
Then AP = PC and DP = PB since the diagonals bisect each other.  Now consider triangles APD and CPB.  The vertical angles APD and CPB are equal, and we have pairs of sides that are equal (AP = PC and DP = PB), so these triangles are congruent by SAS.  As a consequence, the corresponding angles, DAP and BCP are equal.  But these are alternate interior angles for lines AD and BC with transversal AC.  So this proves side AD is parallel to side BC.

Similarly, if we consider triangles APB and CPD, they are congruent by the same reasoning, so corresponding angles BAP and DCP are equal.  These are alternate interior angles for lines AB and DC, so those lines are also parallel.

Therefore ABCD is a parallelogram, by definition.

Theorem 2:  If the diagonals of a quadrilateral bisect each other and have the same length, then the quadrilateral is a rectangle.

Proof:  Since the diagonals bisect each other, we already know (from Theorem 1) that it is a parallelogram, so all we need to prove is that the angles at the vertices are right angles.

Again let the quadrilateral be ABCD with diagonals AC and BD intersecting at P.  Since the diagonals bisect each other, P is the midpoint of both diagonals.  That is, AP = PB and CP = PD.  But the diagonals are also of the same length, so AP + PB = CP + PD, and by substitution this gives us AP + AP = CP + CP, or 2AP= 2CP.  That is, AP = CP.  Likewise, PB = PD.  Consequently, all 4 triangles APD, APB, CPD, and BPC are isosceles.  So angles PAD and PDA are congruent, angles PBC and PCB are congruent, angles PAB and PBA are congruent, and angles PDC and PCD are congruent.  We already saw in the proof of Theorem 1 that triangles APD and CPB are congruent, as are triangles APB and CPD.  By angle addition, it follows that the 4 angles of the quadrilateral (angles ABC, BCD, CDA, and DAB) are all equal.  But the angles of a quadrilateral add to 360^o, and therefore each of these 4 angles must be 90^o.

Theorem 3:  If the diagonals of a quadrilateral bisect each other and are perpendicular then the quadrilateral is a rhombus.

Proof:  Again let the quadrilateral be ABCD with diagonals AC and BD intersecting at P:

Since they bisect each other and are perpendicular, triangles APB, BPC, CPD, and DPA are right triangles.

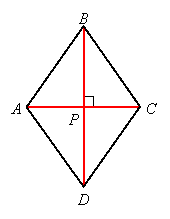
They are all congruent by SAS.  For example, triangle APB is congruent to triangle CPB because they share a common side BD, sides AP and CP are congruent (since P is the midpoint of AC), and the included angles are both right angles.  Since they are all congruent, their third sides (the hypotenuse of each) are congruent (CPCTC).  A rhombus is a quadrilateral in which all four sides are congruent, so ABCD is a rhombus.

Theorem 4:  If the diagonals of a quadrilateral are perpendicular and one bisects the other, then the quadrilateral is a kite.

That is, if the quadrilateral is ABCD with diagonals AC and BC intersecting at P, and if AP = CP, then AB = BC and AD = BD:

Proof:  In this case, triangles APB and CPB are congruent (by SAS), and triangles APD and CPD are congruent.  Therefore AB = BC and AD = CD.