Kaleidoscopes
A typical kaleidoscope contains two mirrors at an angle to each other and a strip of black paper on the third side of the triangle thus formed. The angle at which the mirrors are placed determines how many reflections of an image are seen. For example, suppose the mirrors make an angle of 60o:
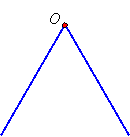
The point of intersection O of the mirrors will not be reflected and is "stationary." A different point P on one of the mirrors will be reflected in the other mirror and be seen as another point P'. Because of this, OP' will be seen as a "virtual mirror."
 |
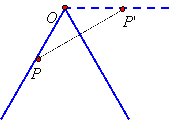If we place a point Q on the other mirror, we see that this virtual mirror extends in both directions:
 |
But then a reflection of point P will also be seen in this virtual mirror as point P'' and a reflection of point Q will also be seen in this virtual mirror as point Q'', so the two mirrors extend in both directions:
 |
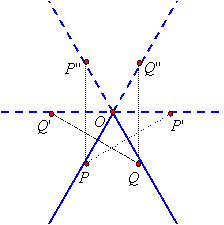Thus the mirrors and their virtual counterparts are three reflection lines, and it follows that any point between the two mirrors will have 5 images, and any hexagon containing the point and its 5 images as vertices will have the three (virtual) mirrors as lines of symmetry. For example:
 |
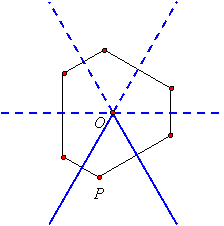It also follows that such a figure will have rotational symmetry, and the angle of rotation will be twice 60o, or 120o.
In general, if the angle between the mirrors measures 180o/n, where n is a whole number, then an image as seen in the kaleidoscope will have n lines of symmetry and rotational symmetry with an angle of rotation equal to twice 180o/n, or 360o/n.
A reference with some attractive kaleidoscope images is: Kaleidoscope
Content ©2009. All Rights Reserved.
Date last modified: March 7, 2009.
Created with SoftChalk LessonBuilder