
Symmetry
Many objects in nature appear the same on the left and right.

The left half of a butterfly appears the same as the right half, and if we were to place a mirror down the center to reflect the left half, the resulting butterfly would look the same as the original:
 |
If we think of the butterfly as a two-dimensional geometric figure, then if we reflect any point on its left side through the vertical line down its center, then we get a corresponding point on the right side. We say the butterfly has line symmetry. That is, it is symmetric with respect to the vertical line through its center.
In general, a geometric figure is symmetric with respect to some line if the reflection of every point through that line is another point on the figure. We say that the figure is "mapped onto itself" by the reflection line.
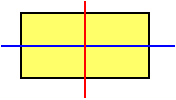
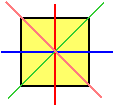
Figures can have more that one line of symmetry. For example, every rectangle has two lines of symmetry, and every square has 4 lines of symmetry:
 |
 |
Rotational Symmetry
A figure has rotational symmetry if it can be mapped onto itself (every point rotates to another point on the figure) by a positive rotation of 180o or less about a point called the "center" of the figure. The angle of rotation is the smallest positive angle through which this happens.
For example, the following "windmill" has rotational symmetry and maps onto itself when rotated through an angle of 60o, 120o, or any other multiple of 60o:
 |
 |
 |
 |
The angle of rotation for this figure is 60o.
Line Symmetry vs Rotational Symmetry
Recall that reflections in two intersecting lines give the same result as a rotation about their point of intersection through twice the acute angle between the two lines. As a consequence, if an object has two lines of symmetry, it must also have rotational symmetry about the point of intersection of those two lines. However, the converse is not true. An object can have rotational symmetry, but not line symmetry. The "windmill" which has 60o rotational symmetry does not have line symmetry. A parallelogram has 180o rotational symmetry (with center the intersection of its diagonals) but no line symmetry:

Kaleidoscopes
A typical kaleidoscope contains two mirrors at an angle to each other and a strip of black paper on the third side of the triangle thus formed. The angle at which the mirrors are placed determines how many reflections of an image are seen. For example, suppose the mirrors make an angle of 60o:
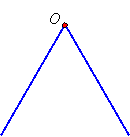
The point of intersection O of the mirrors will not be reflected and is "stationary." A different point P on one of the mirrors will be reflected in the other mirror and be seen as another point P'. Because of this, OP' will be seen as a "virtual mirror."
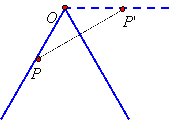 |
If we place a point Q on the other mirror, we see that this virtual mirror extends in both directions:
 |
But then a reflection of point P will also be seen in this virtual mirror as point P'' and a reflection of point Q will also be seen in this virtual mirror as point Q'', so the two mirrors extend in both directions:
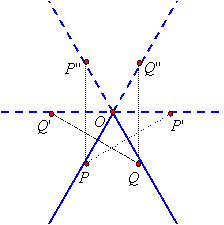 |
Thus the mirrors and their virtual counterparts are three reflection lines, and it follows that any point between the two mirrors will have 5 images, and any hexagon containing the point and its 5 images as vertices will have the three (virtual) mirrors as lines of symmetry. For example:
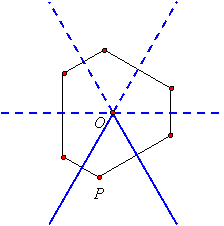 |
It also follows that such a figure will have rotational symmetry, and the angle of rotation will be twice 60o, or 120o.
In general, if the angle between the mirrors measures 180o/n, where n is a whole number, then an image as seen in the kaleidoscope will have n lines of symmetry and rotational symmetry with an angle of rotation equal to twice 180o/n, or 360o/n.
A reference with some attractive kaleidoscope images is: Kaleidoscope
Return to Unit 1