Trig Functions of Any Angle

Though the trig functions were originally defined for acute angles on right triangles, these definitions can be extended to any angles by considering the standard position of an angle.  Of course, if an angle is acute (between 0^o and 90^o) the new definitions should give the same result as the old definitions.

To arrive at a general definition, let us start with an acute angle θ in standard position, and construct a right triangle with a point on its terminal side with coordinates (x, y):

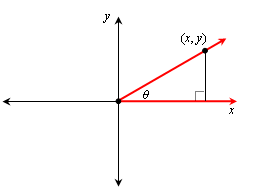
Since x and y are positive, they are the lengths of the legs of the right triangle, and the length of the hypotenuse can be found using the Pythagorean Theorem.  If we call that length r (for reasons that will become apparent), then r² = x² + y².

Then according to the old definitions, we have:

Now the reason we called the hypotenuse r is we can think of the point (x, y) as a point on a circle of radius r centered at the origin:

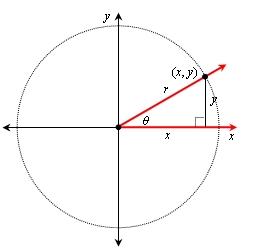
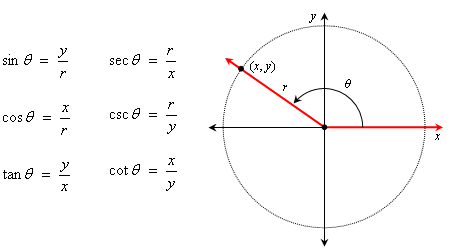
We can use this idea as the general definitions of the trig functions:

If θ is an angle in standard position, construct a circle of radius r centered at the origin, and let (x, y) be the point where the angle's terminal side intersects the circle.  Then:

toc | return to top | next page