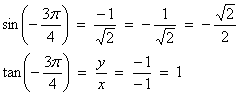
General Definitions of Trig Functions

Trig Functions of Any Angle

Though the trig functions were originally defined for acute angles on right triangles, these definitions can be extended to any angles by considering the standard position of an angle.  Of course, if an angle is acute (between 0^o and 90^o) the new definitions should give the same result as the old definitions.

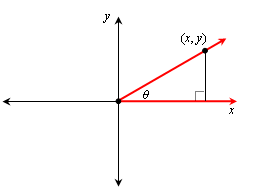
To arrive at a general definition, let us start with an acute angle θ in standard position, and construct a right triangle with a point on its terminal side with coordinates (x, y):

Since x and y are positive, they are the lengths of the legs of the right triangle, and the length of the hypotenuse can be found using the Pythagorean Theorem.  If we call that length r (for reasons that will become apparent), then r² = x² + y².

Then according to the old definitions, we have:

Now the reason we called the hypotenuse r is we can think of the point (x, y) as a point on a circle of radius r centered at the origin:

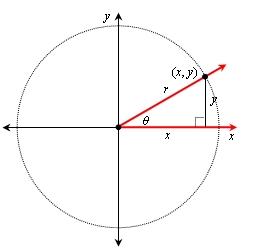
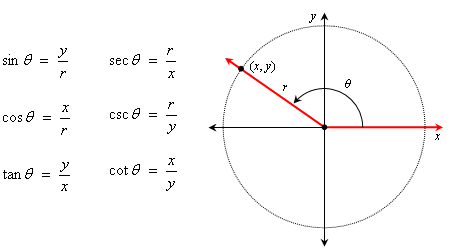
We can use this idea as the general definitions of the trig functions:

If θ is an angle in standard position, construct a circle of radius r centered at the origin, and let (x, y) be the point where the angle's terminal side intersects the circle.  Then:

Example 1:

If (–4, 3) is a point on the terminal side of an angle θ in standard position, find the values of the six trig functions of θ.

Solution:

We draw a picture and find r:

Now we use the definitions of the trig functions:

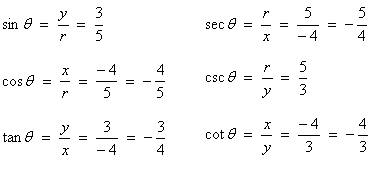
Quadrantal Angles

Quadrantal Angles are angles in which the terminal side is on the x- or y-axis.  We will consider the consequence of our new definitions for such angles first.

Example 2: 

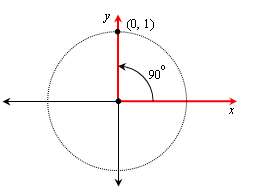
Find the trig functions of 90^o.

Solution: 

We can choose any value of r, so to make it easy, we choose r = 1.  Then the coordinates of the point on the terminal side that intersects our circle will be (0, 1):

Now we use the definitions to find the values of the trig functions.  Notice that some are "undefined" because you cannot divide by 0:

Example 3: 

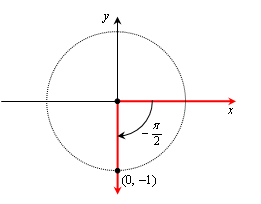
Find the values of the trig functions of 180^o.

Solution: 

Again we use a circle of radius 1:

The point on the terminal side has coordinates (–1, 0), so:

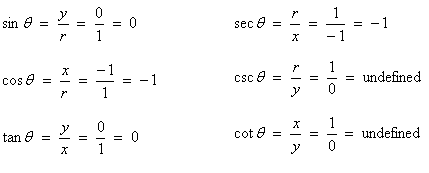
Example 4:

Solution:

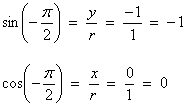
Reference Angles

Every angle that is not quadrantal has what is called a reference angle, and that is the acute angle between the terminal side and the x-axis.  A reference angle is always positive and less than 90^o.  The value of a trig function will always be plus-or-minus the value of the function of the reference angle.  More precisely, the absolute value of a trig function of an angle will always equal the value of the trig function of its reference angle:

Example: 

If θ = 100^o, then the reference angle is 80^o and:

Special Angles

Angles with a reference angle of 30^o, 45^o or 60^o are called "special angles" and the exact values of the trig functions can be found, as the following examples illustrate.

Example 5:

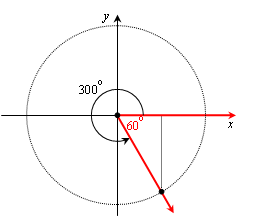
Find the exact values of the trig functions of 300^o.

Solution:

We draw the angle in standard position and find that its reference angle is 60^o:

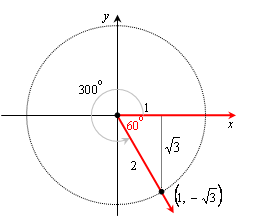
The triangle formed by drawing a perpendicular to the x-axis is a 30-60-90 triangle, so the side opposite the 30 degree angle is half the hypotenuse, so we might as well choose 2 for the length of the hypotenuse, which is our value of r.  Then we have:

Now we can give the exact values of the trig functions:

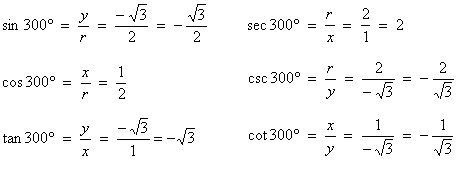
Example 6:

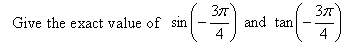
Solution:

The perpendicular from the point on the terminal side gives us a 45-45-90 triangle, so we will choose 1 as the common length of the legs, and then the hypotenuse r has length the square root of 2, and the coordinates of the point on the terminal side are both negative since it is in the 3^rd quadrant:

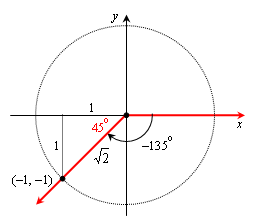
So now we can give the exact values: