The Net of a Frustum

A frustum of a cone is the part of the cone that is left when a plane cuts off the part containing its apex.  There are many practical uses of frustums, such as the following:

A repair man needs to make a frustum of a cone to bridge two circular ducts which are 4 inches apart and have diameters 5 inches and 8 inches:

 

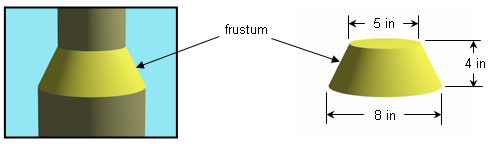
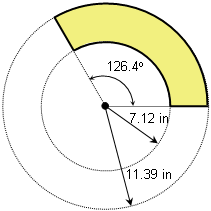
He has a large sheet of thin metal from which he will cut a net that will bend into this frustum, so he needs to know three important dimensions of that net:  the inner radius, r, the outer radius, R, and the angle of the sector, θ:

To figure this out, look at a side view of the frustum in its containing cone:

Looking at similar triangles ABD and DFE, we see that

So h = 6.6667

By the Pythagorean Theorem applied to triangle ABD,

Now we can find R by using similar triangles ACE and ABD:

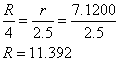
Finally, the sectors are 2.5/r = 4/R of the circle, so

Thus he must use 7.12 inches as the inner radius, 11.39 inches as the outer radius, and cut at an angle of 126.4^o.

toc | return to top | previous page