Drawings and Nets

Hidden Lines and Views

When drawing three dimensional objects, it is customary to show edges that are behind faces with dashed lines.  These are called "hidden lines" or "hidden edges."  For example, the cube on the left would be drawn as on the right, where edges CG, HG, and FG are hidden edges.

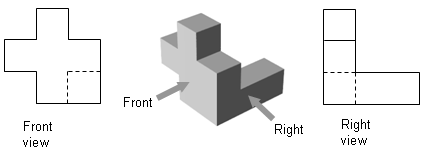
Engineers often draw "views" of solids from various angles.  Here is an example of an object with its front and right views.  Hidden lines are very important in views so the engineer can understand the drawings.

Nets

A net of a geometric solid is a two-dimensional (planar) figure that can be folded into a geometric solid. For example, we know that a cube has six sides. Each side of a cube is a square. So if we arrange six squares into a figure that can be folded into a cube, we have a net for a cube.

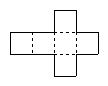
Here are a few examples of nets of cubes:

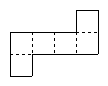
However, not every figure of six squares can be folded into a cube. Here are some figures that are not nets of cubes:

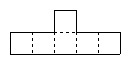
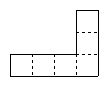
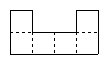
Nets are useful for find the surface area of a polyhedron, as the following examples illustrate.

Example 1:

Find the total surface area of the square pyramid in which each edge measures 18 ft:

Solution:

We draw a net of this pyramid and then find the areas of each of the 4 triangles and the square in the middle:

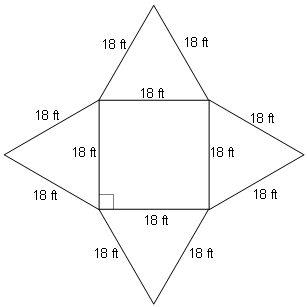
The area of the square is 18∙18 = 324 square feet, so the total surface area of the pyramid is:

Example 2:

Find the lateral surface area of a right cone whose base is a circle of diameter 10 inches and whose altitude is 12 inches:

Solution:

A net for the cone's lateral surface is a sector of a circle.  The radius of that circle is the slant height of the cone, and we can find that by the Pythagorean Theorem:

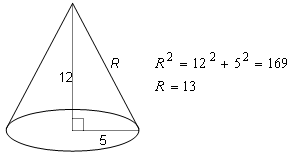
The circumference of the base is the length of the sector that forms the net, and is 10π.  The circumference of the circle containing that sector is 26π, so the sector is 10/26 or 5/13 of its circle and is subtended by an angle of 5/13 of 360^o, or about 138.5^o:

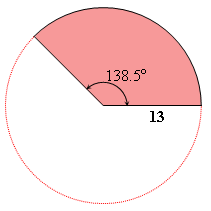
Therefore, the area of the sector is 5/13 the area of the circle with radius 13 inches, or about 204.2 square inches.

The Lateral Area of a Right Cone

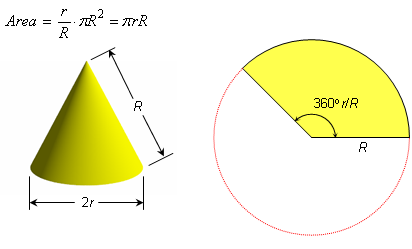
The previous example can be used to derive a formula for the lateral area of any cone.  If the slant height of a cone is R units and the radius of the base is r units, then a net for the cone's lateral surface is a sector that is r/R of a circle of radius R, and its area simplifies as:

The Net of a Frustum

A frustum of a cone is the part of the cone that is left when a plane cuts off the part containing its apex.  There are many practical uses of frustums, such as the following:

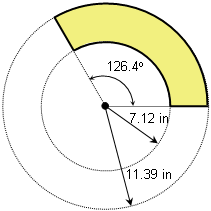
A repair man needs to make a frustum of a cone to bridge two circular ducts which are 4 inches apart and have diameters 5 inches and 8 inches:

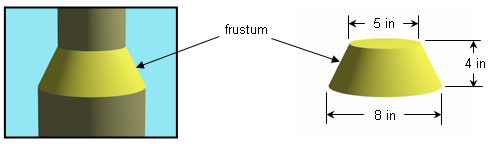
He has a large sheet of thin metal from which he will cut a net that will bend into this frustum, so he needs to know three important dimensions of that net:  the inner radius, r, the outer radius, R, and the angle of the sector, θ:

To figure this out, look at a side view of the frustum in its containing cone:

Looking at similar triangles ABD and DFE, we see that

So h = 6.6667

By the Pythagorean Theorem applied to triangle ABD,

Now we can find R by using similar triangles ACE and ABD:

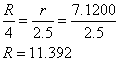
Finally, the sectors are 2.5/r = 4/R of the circle, so

Thus he must use 7.12 inches as the inner radius, 11.39 inches as the outer radius, and cut at an angle of 126.4^o.