Construct a triangle given SAA

It is a littler trickier to construct a triangle given a side and two angles if the angles do not include the side.  To do this we make use of the proof that the sum of the angles of a triangle is 180^o.  Recall that such a proof depends on the parallel postulate and the alternate interior angle theorem.

Given:  Side AB, and angles A and C, construct triangle ABC.

 

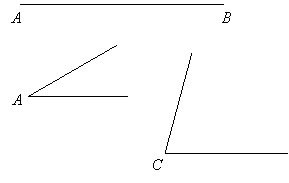
Solution:

Mark off segment AB and construct two copies of angle A, one with vertex A and one with its vertex at B.  This gives two parallel lines, AD and BE:

Now construct a copy of angle C at vertex B and side BE as follows:

 

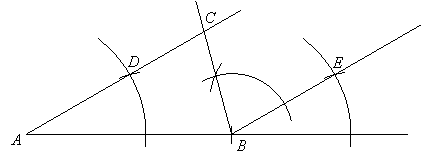
The new side of this angle intersects line AD at point C, and angle ACB is congruent to angle CBE since these are alternate interior angles for parallel lines AD and BE.  Therefore, triangle ABC has the correct side and angles.

toc | return to top | previous page