Constructing Triangles

Construct a Triangle given SAS

If you are given two sides and the included angle for a triangle, you can construct it by making a copy of one of the sides, copying the angle with its vertex at an endpoint of the side, then marking off the length of the other side, and finally constructing the third side.

Given:  Sides AB and AC, and angle A, construct triangle ABC:

Solution:

Draw a segment longer than AB, label one endpoint as A, and use the compass with its radius set to the length of AB to mark off point B:

Then construct a copy of angle A at the endpoint A:

Next mark off point C using AC as the radius of the compass and point A as the center.

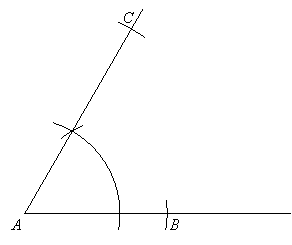
Finally construct side BC by placing the straight-edge at points B and C:

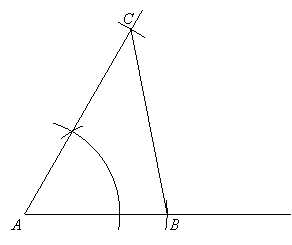Here is a an animation of this construction.

Construct a triangle given ASA

If you are given two angles and the included side of a triangle, you can construct the triangle as follows:

Given:  Side AB, and angles A and B, construct triangle ABC.

Solution:

First construct side AB by drawing a line slightly longer and marking off the right length using the compass:

Next copy angle A:

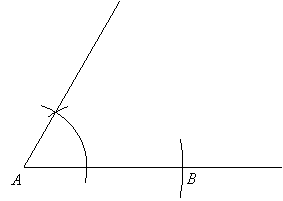
Finally, copy angle B.  Be sure to put the point of the compass at B when drawing the first arc.  The intersection of the copied sides of the angles is point C:

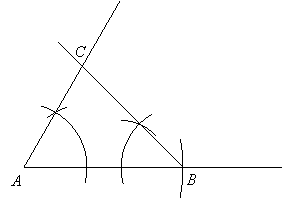Here is an animation for this construction.

Construct a triangle given SSS

If you are given the three sides of a triangle, you can construct it as follows.

Given:  Sides AB, AC and BC, construct triangle ABC.

Solution:

First construct one of the sides—say AB:

Next set the compass to radius AC and draw an arc with center A:

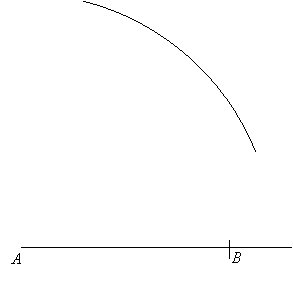
Then set the compass to radius BC, place its point at B on the constructed line, and draw another arc so it intersects the previous arc giving point C:

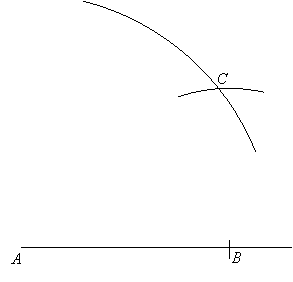
Finally, use the straight-edge to draw sides AC and BC.

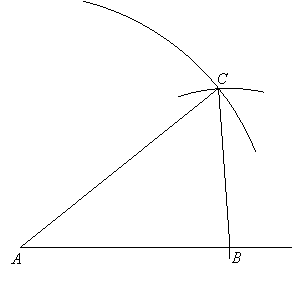
Here is an animation showing this construction.

Construct a triangle given SAA

It is a littler trickier to construct a triangle given a side and two angles if the angles do not include the side.  To do this we make use of the proof that the sum of the angles of a triangle is 180^o.  Recall that such a proof depends on the parallel postulate and the alternate interior angle theorem.

Given:  Side AB, and angles A and C, construct triangle ABC.

Solution:

Mark off segment AB and construct two copies of angle A, one with vertex A and one with its vertex at B.  This gives two parallel lines, AD and BE:

Now construct a copy of angle C at vertex B and side BE as follows:

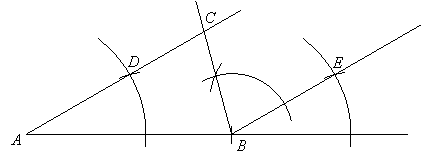
The new side of this angle intersects line AD at point C, and angle ACB is congruent to angle CBE since these are alternate interior angles for parallel lines AD and BE.  Therefore, triangle ABC has the correct side and angles.

Return to Lesson 9