The Six Trigonometric Functions

Example 1:

A hot air balloon is flying at an altitude of 500 feet.  A passenger sees to buildings directly to his left and uses a transit to measure the angles of depression to those buildings, as shown:

How far apart are the buildings?

Solution:

Since the angles of depression are equal to the angles of elevation (they are alternate interior angles for the parallel horizontal lines), we can use two right triangles, BAC and BAD to find the lengths of AC and AD using the tangents of angles BCA and BDA:

For triangle BAC,

For triangle BAD,

Since CD = AD – AC = 1072 – 714 = 358

The buildings are 358 feet apart.

Example 2:

If θ is an acute angle and sin θ = 0.2000, find the values of cos θ and tan θ to four significant figures.

Solution:

We can use any right triangle in which the ratio of opposite side to hypotenuse is 0.2000, so we will choose one in which the hypotenuse is 1:

We use the Pythagorean Theorem to find the length of the adjacent side:

x² + (0.2000)² = 1²

x² = 0.96

x = 0.9798

Now we can use the definitions to find cos θ and tan θ:

 Example 3:

Triangle ABC is a right triangle,  AB = 60 units, and

.

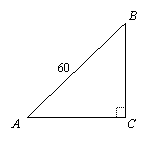
a.  How long is AC? 

b.  How long is BC?  (Give a simplified, exact answer.)

Solution:

The sine of an acute angle in a right triangle is the ratio of the opposite side to the hypotenuse, so we know that the ratio of AC to 60 is 2 to 3:

Cross-multiplying and solving for AC:  3AC = 120,  AC = 40

To find BC, we can use the Pythagorean Theorem:

BC² + 40² = 60²,  BC² = 2000,  so

Example 4:

Suppose triangle DEF is a right triangle, and  EF is twice as long as DF.

What are the values of the 6 trig functions of angle D?

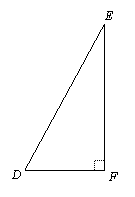
Solution:

Since trig functions are ratios, they are "unit-free."  Therefore it does not matter what size the triangle is, as long as the ratios are correct.  We can choose DF to be one unit in length, so EF will be two units, and we can use the Pythagorean Theorem to find DE is the square root of 5:

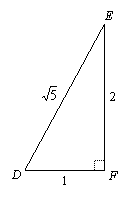
Now we can give the values of the trig functions:

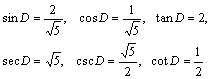
Example 5:

What is the area of a regular pentagon whose sides measure 10 cm?

Solution:

The area of any regular polygon is the half the product of its apothem and perimeter, so we need to find the length of the apothem, OP:

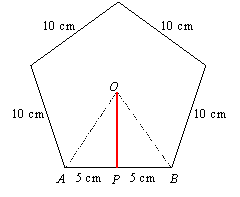
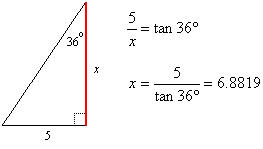
We could construct 5 triangles such as AOB in the pentagon, and each contains two congruent triangles, such as AOP and BOP.  There would then be 10 congruent angles with vertex O, and their sum would be 360^o.  Therefore each angle measures 36^o.  In particular, angle AOP is 36^o, so we can use the tangent function on triangle AOP to find the apothem:

Now we can find the area of the pentagon.  Its perimeter is 50 cm, so its area is:

Return to Lesson 12