Transformations

Transformations

A transformation is an operation on a geometric figure that transforms it into a new (or possibly the same) geometric figure.  Such an operation is sometimes called a "mapping" and we say that a figure is "mapped" by a transformation into its "image."  The original figure is called the "preimage" of the transformation.

For example, if we draw a triangle on a sheet of rubber and then stretch it horizontally, the resulting figure is a transformation of the triangle:

This stretch transformation changes the shape of the triangle, so the image is just a different triangle, not congruent or similar to the original triangle.

Isometries

There are three main types of transformations that do NOT change the size or shape of a figure, and these are called isometries.  A figure and its image are therefore congruent when the transformation is an isometry.

A translation merely moves the figure to a different location.  That is, every point of the figure is moved the same distance and direction as every other point:

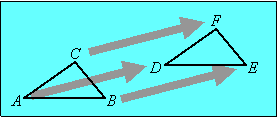Triangle ABC is translated to triangle DEF.  Each vertex of the preimage (triangle ABC) is moved the same distance and direction to the corresponding vertex of the image (triangle DEF).

A rotation turns a figure through a certain angle about a fixed point, called the center of rotation.  That point need not be a point on the figure itself, and every point of the figure is rotated through the same angle about the center of rotation:

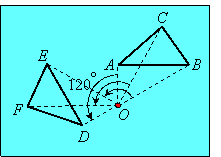Notice that each vertex of the preimage (triangle ABC) has been rotated about point O through a counterclockwise angle of 120^o.

The angle of rotation is positive when it is measured counterclockwise, and negative when measured clockwise.

A reflection uses a line of reflection to create a mirror image of the original figure.  Each point of the preimage and the corresponding point of the image are the same distance (as measured perpendicularly) from the line of reflection:

Composition of Transformations

Two or more transformations can be applied successively to obtain a new figure.  When those transformations are isometries, the resulting figure is congruent to the original figure.

Example:  Rotate triangle ABC through –90^o using P as the center of rotation, then reflect the image through line l to obtain triangle DEF:

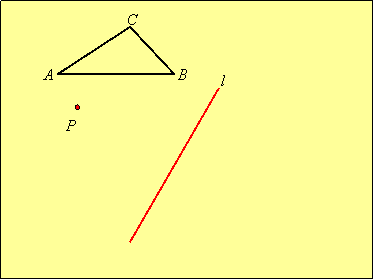Solution:  First we rotate each vertex around point P.  We will label the vertices of the image with primes:

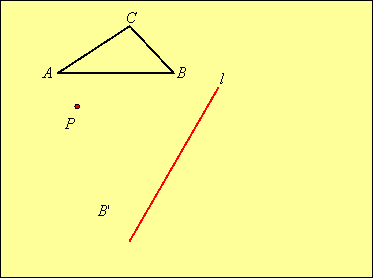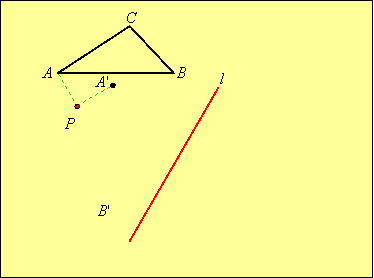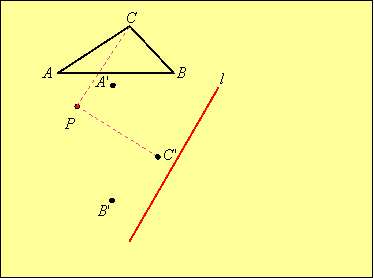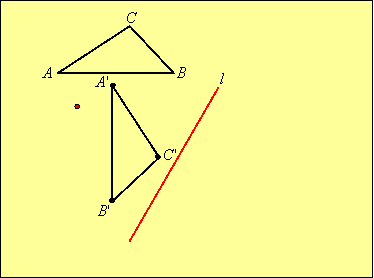
Then we reflect this image in line l by first reflecting each vertex in l and then joining the vertices: 

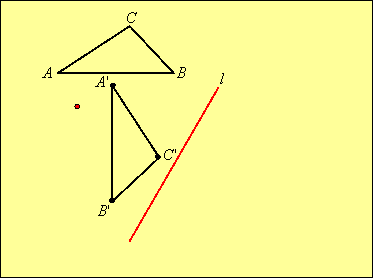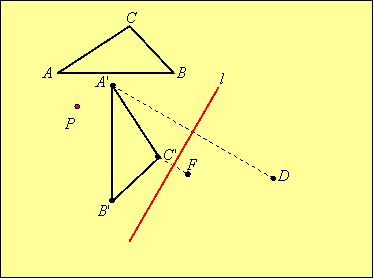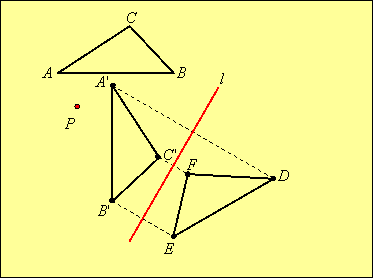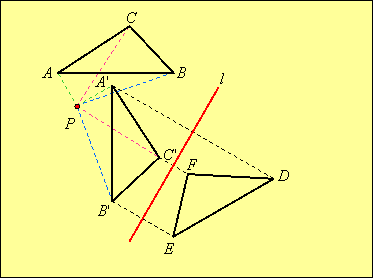
Return to Lesson 4