Solving Quadratic Equations by Factoring

FOIL

When two binomials are multiplied, their product can be expanded by FOIL.

The letters stand for First, Outer, Inner, Last.

The following examples illustrate the use of FOIL:

Example 1:  Expand (2x + 5)(3x + 4)

Solution:

We multiply 2x by each of the terms in 3x + 4 and then multiply 5 by each term in 3x + 4, and combine the like terms in the middle.  2x and 3x are the First terms of each binomial, 2x and 4 are the Outer terms, 5 and 3x are the Inner terms, and 5 and 4 are the Last terms.

The pattern for FOIL is:

We get:  (2x + 5)(3x + 4) = 6x² + 23x + 20

Example 2:  Expand:  (x – 3)(2x + 1)

Solution: 

Think of this as:  (x  +  –3)(2x  +  1)

Using FOIL:

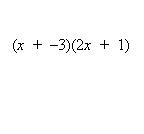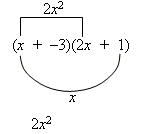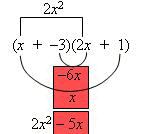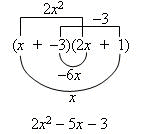
So (x – 3)(2x + 1) = 2x² – 5x – 3

Example 3:  Expand:  (3x – 2)(3x + 2)

Solution:

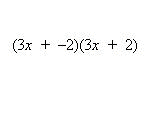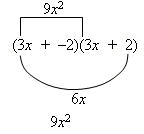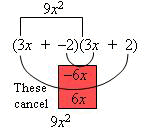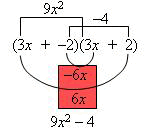
This example illustrates that a difference of two terms times the sum of the same two terms results in the difference of the squares of those two terms.  In general, the following binomial products should be recognized as the outer and inner terms cancel:

(a – b)(a + b) = a² – b²

(a + b)(a – b) = a² – b²

Reverse FOIL

"Reverse FOIL" is a method of factoring a quadratic trinomial by trial-and-error.  The strategy is to determine the First and Last terms of each binomial in the factored product so the Outer and Inner products add to the middle term.

The following examples illustrate this.

Example 4:  Factor  3x² + 5x – 12

Solution:  First we concentrate on 3x² and –12.  3x² is the product of 3x and x, so we place these First terms of the factors:

3x² + 5x – 12 = (3x           )(x          )

Now –12 could result in many different ways.  It could be –1 times 12, –2 times 6, 2 times –6, or any number of other products.

To make it easier, we ignore the negative for the time being and try various products that give 12, and then ask ourselves if it is possible to get the middle term, 5x, by subtracting the Outer and Inner products:

3x² + 5x – 12 = (3x           2)(x          6)

                          Outer = 18x, Inner = 2x  No

3x² + 5x – 12 = (3x           6)(x          2)

                          Outer = 6x, Inner = 6x  No

3x² + 5x – 12 = (3x           4)(x          3)

                          Outer = 9x, Inner = 4x  Yes, 9x – 4x = 5x

So we want the 4x to be negative.  Therefore the factorization is:

3x² + 5x – 12 = (3x – 4)(x + 3)

Example 5:  Factor  6x² – 23x + 20

Solution: We concentrate on 6x² and 20 first.

6x² could result from 6x times x or from 3x times 2x.

Let's try 3x times 2x and worry about the 20:

6x² – 23x + 20 = (3x         )(2x         )

20 could be 2 times 10, 10 times 2, 4 times 5, 5 times 4, 1 times 20, or 20 times 1.  Since the middle term is negative, both factors of 20 should be negative.

Let's try –2 times –10:

(3x – 2)(2x – 10) = 6x² – 34x + 20

The middles add to –34x which is wrong.

So we try –5 times –4:

(3x – 5)(2x – 4) = 6x² – 24x + 20

Close, but not right.  The middles should add to –23x, not –24x.

Try –4 times –5:

(3x – 4)(2x – 5) = 6x² – 23x + 20

This is right, so we know 6x² – 23x + 20 factors as (3x – 4)(2x – 5)

Factoring a GCF first

Sometimes a trinomial has a greatest common factor.  When this is the case, we should first factor that, and then apply reverse FOIL.

Example 6:  Factor 6x² – 2x – 4

Solution: Every term is a multiple of 2.  That is, 2 is a greatest common factor, so we first factor that:

6x² – 2x – 4 = 2(3x² – x – 2)

Then we factor the trinomial in parentheses:

6x² – 2x – 4 = 2(3x² – x – 2) = 2(3x + 2)(x – 1)

The Difference of Squares 

Some quadratic binomials are the difference of two perfect squares.  When this is the case, they can be factored as a difference times a sum, and the following formula applies:

a² – b² = (a – b)(a + b)

Example 7:  Factor 9x² – 4

Solution:  9x² = 3x ^. 3x and 4 = 2 ^. 2, so this binomial is the difference of two squares.  It factors as:

9x² – 4 = (3x – 2)(3x + 2)

Example 8:  Factor 3x² – 48

Solution:  3x² and 48 are not perfect squares, but both have 3 as a common factor.  Therefore we start by factoring out 3:

3x² – 48 = 3(x² – 16)

Now x² – 16 is the difference of squares, so it can be factored:

3x² – 48 = 3(x² – 16) = 3(x – 4)(x + 4)

Solving Equations by Factoring

When the product of two numbers is 0, then one of the numbers must be 0.  This is a special property of 0 and does not apply to other numbers.  For example, if the product of two numbers is 8, then neither number need be 8 (2 times 4 is 8, so the numbers could be 2 and 4).

This property of 0 is called the "zero product property" and can be used to solve an equation when its factored form is equal to 0.

For example, the equation (x – 5)(x + 3) = 0 tells us that the product of the two numbers x – 5 and x + 3 is 0.  Therefore one of these numbers must be 0.  That is, either x – 5 = 0 or x + 3 = 0.  The solutions to these two equations are x = 5 and x = –3, so the equation (x – 5)(x + 3) = 0 has these two solutions.

Quadratic equations of the form ax² + bx + c = 0 can often be solved by factoring the left side, as the following examples illustrate.

Example 9:  Solve x² + 3 = 4x

Solution:  First subtract 4x from both sides to get:

 x² – 4x + 3 = 0

Then factor the left side:

(x – 1)(x – 3) = 0

Now set each factor to 0 and solve:

x – 1 = 0   -->  x = 1

x – 3 = 0   -->  x = 3

Example 10:  Solve (2x – 3)(x + 5) = 7

Solution:  We cannot conclude that one of the factors on the left is 7, since 7 does not share the 0 product property.  So we must expand the left side, subtract 7, and then factor the left side:

(2x – 3)(x + 5) = 7

2x² + 7x – 15 = 7

2x² + 7x – 22 = 0

(2x + 11)(x – 2) = 0

Now set each factor equal to 0 and solve:

2x + 11 = 0   -->   2x = –11  -->   x = –5.5

x – 2 = 0   -->   x = 2

Return to Lesson 2