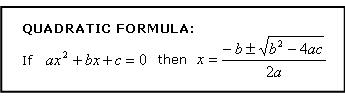
The Quadratic Formula
The Formula
A quadratic equation is an equation that can be written in the form ax2 + bx + c = 0, where a, b and c are numbers. As we saw in the previous activity, some quadratic equations can be solved by factoring and using the fact that if the product of two numbers is 0, then one of the numbers must be 0.
Not all quadratic trinomials can be factored, and you might be uncomfortable with factoring anyway. A sure method for finding the solutions (also called "roots") of a quadratic equation is to use the quadratic formula:
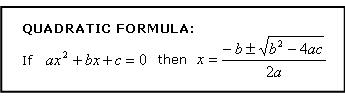
Example 1: Solve: 5x2 + 6x – 8 = 0
Solution:
In this equation, a = 5, b = 6, and c = –8, so plug these values in the formula:
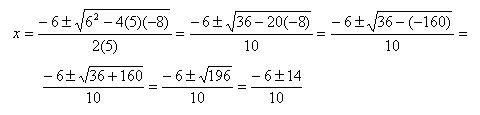
There are two solutions:
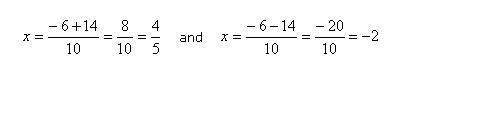
Example 2: Solve: x(x – 2) = 2
Solution:
First expand the left side, then subtract 2 from both sides to get x2 – 2x – 2 = 0.
This is the same as 1x2 – 2x – 2 = 0, so a = 1, b = –2, and c = –2. Plug these values in the quadratic formula:
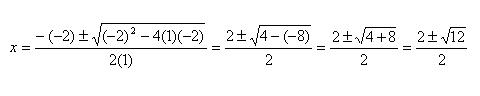
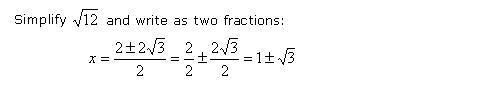
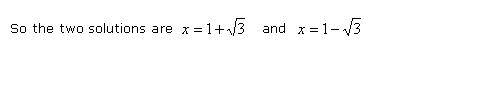
Example 3: The sum of two numbers is 6 and their product is 7. What are those numbers?
Solution:
If one of the numbers is x, then the other must be 6 – x since they add to 6. If their product is 7, then we have the equation x(6 – x) = 7.
Expanding gives 6x – x2 = 7. If we subtract 7 from both sides, we get :
–x2 + 6x – 7 = 0
Whenever an equation begins with a negative x2, it is best to multiply both sides by negative one so it begins with a positive x2. So we do that and get:
x2 – 6x + 7 = 0
Now we use the quadratic formula:
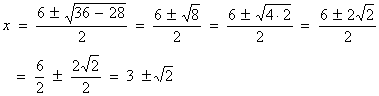
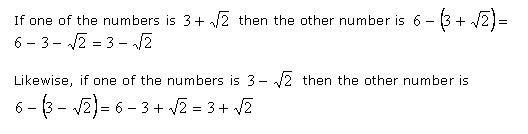
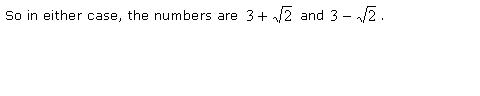
Example 4: Solve: x2 – 9 = 0
Solution:
Whenever an equation is missing the x-term, it is easier to NOT use the quadratic formula. In this problem we can factor the left side as the difference of squares and then use the zero-product property to solve:
(x – 3)(x + 3) = 0
x – 3 = 0 --> x = 3
x + 3 = 0 --> x = –3
We could also rewrite this equation as x2 = 9 and then take the square roots of both sides, but remember that there are two square roots of any positive number – one positive and one negative:
x2 = 9 --> x = 3 and x = –3
Example 5: Solve: x2 = 5
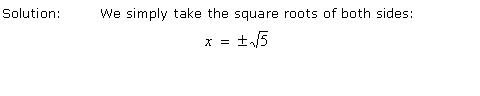
Return to Lesson 2